Deep & Cross Network for Ad Click Predictions (KR)

참고자료

• 원 논문 (Deep & Cross Network for Ad Click Predictions)
  • Deep & Cross Network for Ad Click Predictions

들어가기 전에 알아야될 용어

• deepCTR 라이브러리

ABSTRACT

• 피쳐 엔지니어링은 많은 예측 모델의 성공의 열쇠입니다. 수동으로 하는 피쳐 엔지니어링 또는 철저한 검색이 필요합니다.
• DNN은 자동으로 기능의 상호 작용을 학습할 수 있습니다. 그러나 모든 상호 작용을 암시적으로 생성하므로 모든 유형의 교차 기능을 학습할 때 반드시 효과적일 수는 없습니다.
• 본 논문에서는 DNN 모델의 장점을 유지하는 딥 앤 크로스 네트워크 (Deep & Cross Network, DCN)를 제안하고, 그 외에도 일정한 바운드 (bounded degree) 기능 상호 작용을 학습할 수 있는 새로운 크로스 네트워크를 소개한다.
• 특히 DCN은 각 계층에서 기능 교차를 명시적으로 적용하고 수동 피처 엔지니어링을 필요로 하지 않으며 DNN 모델에 추가 복잡성을 거의 추가하지 않습니다.
• 실험 결과는 모델 정확도와 메모리 사용 면에서 CTR 예측 데이터 세트와 밀도가 높은 분류 데이터 세트에 대한 최첨단 알고리즘보다 우수하다는 것을 보여주었습니다.

1. INTRODUCTION

• 클릭률(CTR) 예측은 수십억 달러 규모의 온라인 광고 산업에 필수적인 대규모 문제입니다. 광고주가 게시자의 사이트에 광고를 게재하도록 게시자에게 비용을 지불합니다.
• 한 가지 인기있는 지불 모델은 클릭이 발생할 때만 광고주에게 비용이 청구되는 클릭당 비용(CPC) 모델입니다. 결과적으로 게시자의 수익은 CTR을 정확하게 예측할 수 있는 능력에 크게 의존합니다.
• 예측되는 기능을 식별하고 동시에 보이지 않는 희귀한 교차 기능을 탐색하는 것은 좋은 예측을 내리는데 핵심입니다.
  • 그러나 웹스케일 추천 시스템의 데이터는 대부분 이산되고 범주적이며 특성 탐색에 어려움을 겪는 크고 드문 기능 공간을 초래합니다.
• 로지스틱 회귀 (logistic regression)와 같은 선형 모델로는 대부분의 대규모 시스템이 제한되어 있습니다.
  • 선형 모델은 간단하고 해석하기 쉽고 확장이 쉽습니다. 그러나 그들은 표현력이 제한적이다.
• 다른 한편으로 Cross features은 모델의 표현력을 향상시키는데 중점을 두는 것으로 나타났습니다.
  • 불행히도 이러한 기능을 식별하려면 수동 기능 엔지니어링 또는 철저한 검색이 필요합니다. 또한 보이지 않는 기능에 상호 작용을 일반화하는 것은 어렵습니다.
• 본 논문에서는 자동으로 피쳐 횡단(feature crossing)을 적용하는 새로운 신경망 구조(교차 네트워크)를 도입
• 교차 네트워크는 여러 계층으로 이루어져 있으며 가장 높은 수준의 상호 작용이 계층 깊이에 따라 결정됩니다.
  • 각 계층은 기존 계층을 기반으로 한 고차원 상호 작용을 생성하고 이전 레이어와의 상호 작용을 유지합니다.
• 깊은 신경망 (deep neural network, DNN) 과 함께 교차망(cross network)을 훈련시킨다.
  • DNN은 기능 간에 매우 복잡한 상호 작용을 포착하지만 그러나 교차 네트워크에 비해 더 많은 매개 변수가 필요하여 Cross features을 형성할 수 없습니다.
  • 명시적으로, 일부 유형의 기능 상호 작용을 효율적으로 학습하지 못할 수 있습니다.
• 그러나 교차 및 DNN 구성 요소를 같이 훈련하면 예측 기능 상호 작용을 효율적으로 캡처합니다. (Criteo CTR 데이터 세트에 최첨단 성능을 제공)

1-1. Related Work

• 데이터 세트의 크기와 차원의 급격한 증가로 인해 대부분 임베딩 기술과 신경망을 기반으로 한 광범위한 작업별 피쳐 엔지니어링을 피하기 위해 여러가지 방법이 제안되었습니다.

1. Factorization machines(FM) : 저밀도 벡터에 희소한 특징을 투영하고 벡터 inner product으로부터 특징 상호 작용을 학습

2. Field-aware factorization machines (FFMs) : 특징이 각 벡터가 어떤 필드와 연관되어 있는 여러 벡터를 학습하도록 한다.

• 대표적인 FMs와 FFMs의 얕은 구조는 추천시스템 파워를 제한합니다. FM을 더 높은 차수로 확장하는 작업이 있었지만, 단점은 많은 양의 매개변수에 놓여있어 바람직하지 않은 계산 비용을 초래합니다.
• DNN는 벡터 및 비선형 활성화 함수로 인해 중요한 특징 상호 작용을 학습할 수 있습니다. Residual Network의 최근 성공은 매우 깊은 네트워크의 훈련을 가능하게 했음
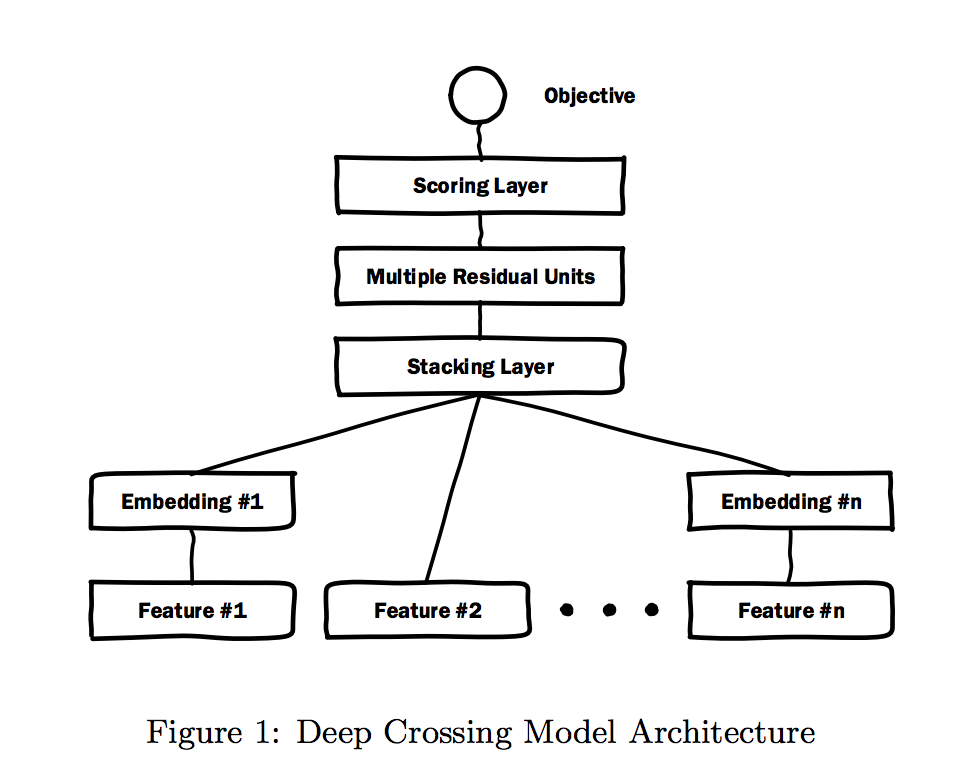
• Deep Crossing은 Residual Network를 확장하고 모든 유형의 입력을 스태킹하여 자동 피쳐 학습을 수행합니다.
• 딥러닝의 눈부신 성공은 이론적으로 도출되었다.
  • DNN은 충분히 많은 숨겨진 유닛이나 숨겨진 레이어가 주어진 임의의 정확도로 특정 매끄러운 가정 하에 임의의 함수를 근사할 수 있다는 연구가 있었음
  • 더욱이 실제로 DNN은 실현 가능한 매개변수의 수와 함께 잘 작동한다는 것이 밝혀졌습니다. ( 실질적인 관심의 대부분의 기능이 임의적이지 않다는 것 )

• Kaggle 경쟁에서 많은 사람들이 handcrafted 기능을 통해서 이기는 솔루션은 명시적인 형식으로 효과적입니다
  • 반면 DNN에서 배운 기능은 내재적이며 매우 비선형적이라 모델을 디자인할 때 빛을 내는 형태
  • bounded-degree feature interactions을 보다 효율적으로 학습할 수 있음
• 범용 DNN보다 명시적으로 wide-and-deep 모델은 선형 모델의 입력으로 교차 피쳐를 사용하고 선형 모델을 DNN 모델과 함께 훈련합니다.
  • 그러나 크로스 피처의 적절한 선택에 대한 wide-and-deep 모델의 경우에는 힌지(hinge) 최적화의 성공이 필요하며, 아직까진 명확한 효율적인 방법이 없는 기하 급수적인 문제로 밝혀지고 있습니다.

1-2. Main Contributions

• 본 논문에서는 희소 및 고밀도 입력을 이용한 웹스케일 자동 특징 학습을 가능하게 하는 Deep & Cross Network (DCN) 모델을 제안

• DCN은 bounded degrees의 효과적인 피쳐 상호 작용을 효율적으로 포착하고 고도의 비선형 상호 작용을 학습하며 수작업 엔지니어링이나 철저한 검색이 필요없고 계산 비용이 적습니다.

• 이 논문의 주요 공헌 내용은 다음과 같습니다.

1. 명시적으로 기능을 적용하는 새로운 교차 네트워크를 제안합니다.
   • 각 레이어에서 교차하여 예측 교차 기능을 효율적으로 학습합니다. 제한된 degrees를 가지며 수동 피처 엔지니어링이 필요하지 않습니다.
2. 교차 네트워크는 간단하면서도 효과적입니다.
   • 디자인 상으로는 다항식 차수는 각 층에서 증가하며 레이어 깊이. 네트워크는 cross terms of degree로 구성됩니다. 최대값, 계수는 모두 다릅니다.

3. 교차 네트워크는 메모리 효율적이며 구현하기 쉽습니다.

4. 실험 결과에 따르면 교차 네트워크에서 DCN은 DNN보다 로그 손실이 적고 매개 변수의 수는 거의 감소했습니다.

• 이 논문은 다음과 같이 구성됩니다, 2 장에서는 Deep & Cross Network의 아키텍처에 대해 설명합니다. 3 장에서는 교차 네트워크를 상세히 분석한다. 4 절에서는 실험 결과를 설명합니다.

2. DEEP & CROSS NETWORK (DCN)

• 이 섹션에서는 DCN (Deep & Cross Network) 모델의 아키텍처에 대해 설명합니다.
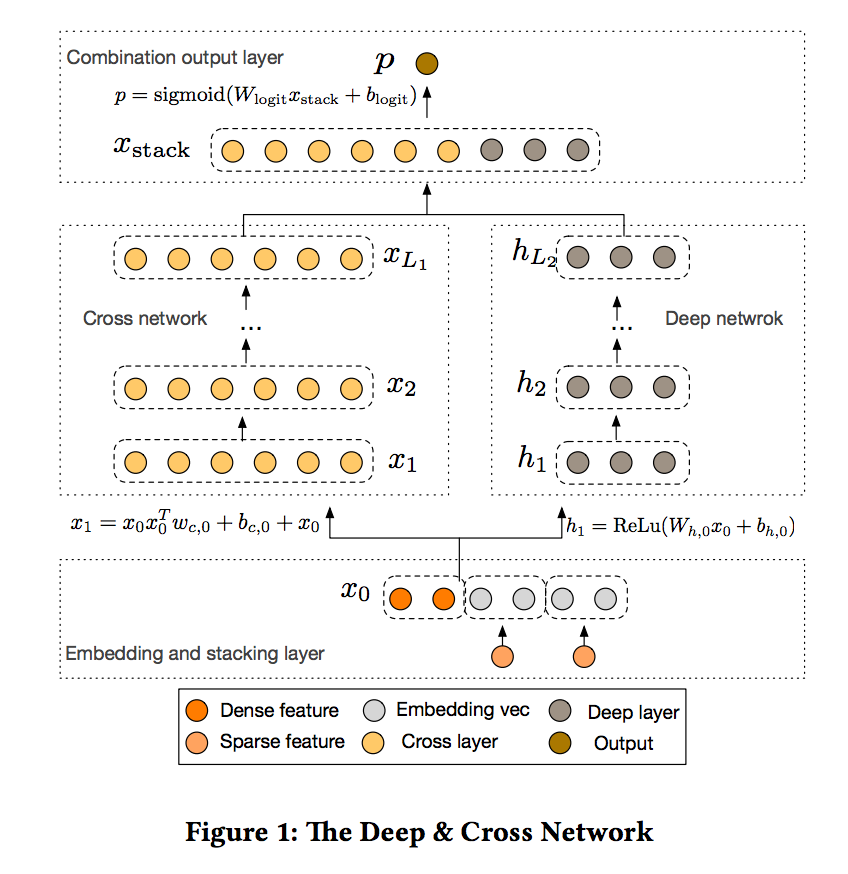
• DCN 모델은 embedding 및 스태킹 레이어부터 시작하여 크로스 네트워크 및 심층 네트워크가 병렬로 구성됩니다.
• 두 네트워크의 출력을 결합한 최종 조합 레이어가 차례로 나타납니다. 완전한 DCN 모델은 그림 1에 묘사되어 있습니다.

2-1. Embedding and Stacking Layer

• 희소하고 밀도가 높은 특성을 가진 입력 데이터를 고려합니다.

• CTR 예측과 같은 웹스케일 추천 시스템에서 입력은 주로 범주형 기능입니다. “country = usa”. 이러한 특징은 종종 예를 들어, 원핫 벡터로 인코딩된다. “[0,1,0]”;

• large vocabularies에 대해 지나치게 높은 차원의 특징 공간을 초래한다.
  • 차원을 줄이기 위해 이진 특성을 실제 값의 고밀도 벡터(일반적으로 embedding 벡터라고 함)로 변환하는 embedding 절차를 사용합니다.

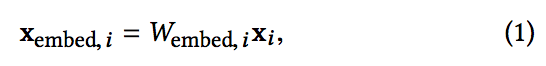
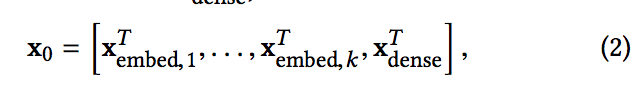
2-2. Cross Network

• 새로운 교차 네트워크의 핵심 아이디어는 명시적 기능을 적용하는 것, 효율적인 방식으로 교차, 교차 네트워크는 각 층은 다음의 공식을 갖는다

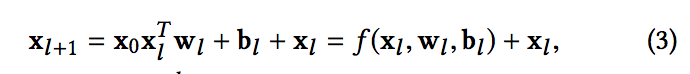
• 각 l 번째 및 l + 1 번째 크로스 레이어로부터의 출력을 나타내는 열 벡터
• l번째 레이어의 가중치 및 바이어스 매개 변수입니다. 각각의 크로스 레이어는 입력을 f를 가로지르는 피쳐와 매핑함수 f를 더합니다.
• 하나의 크로스 레이어의 시각화가 그림 2에 나와 있습니다.

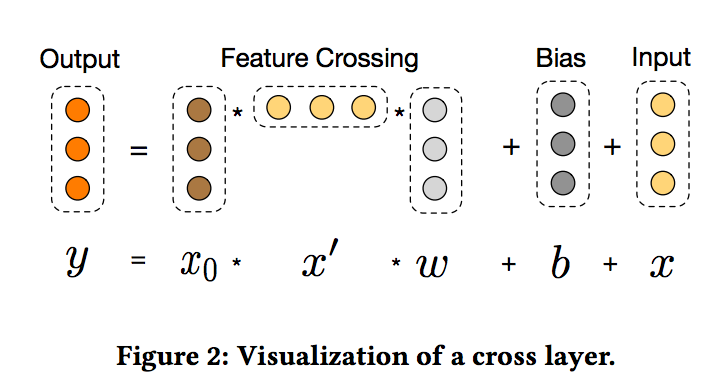
• High-degree Interaction Across Features
  • 크로스 네트워크의 특별한 구조는 레이어 깊이와 함께 교차 피쳐의 정도를 증가시킵니다. (element-level interaction)
  • 사실, 크로스 네트워크는 모든 교차항을 포함한다. x dimension는 1부터 l + 1까지의 차수이다. 상세한 분석은 3장의 복잡도 분석에 있다.
• Complexity Analysis
  • Lc는 교차 레이어의 수를 나타내며, d는 입력 차원을 나타냅니다.
  • 교차 네트워크에 관련된 파라미터의 수는 d × Lc × 2이다.
• 교차 네트워크의 시간과 공간의 복잡성은 입력 차원에서 선형적
  • 따라서 교차 네트워크는 기존의 DNN과 동일한 수준의 DCN에 대한 전반적인 복잡성을 유지하면서 딥러닝 네트워크에 비해 무시할 수 없는 복잡성을 초래함
  • 컴퓨팅이나 저장없이 모든 교차 용어를 생성할 수 있습니다.
  • 전체 행렬 교차 네트워크의 매개변수 수가 적기 때문에 모델 용량이 제한됩니다.
  • 높은 비선형 상호 작용을 포착하기 위해 우리는 깊은 네트워크를 병렬로 도입합니다.

2-3. Deep Network

• 딥 네트워크는 완전히 연결된 피드 포워드(feed-forward) 신경망으로, 각각의 deep layer은 다음의 공식을 갖는다.

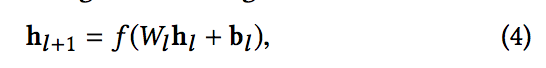
• f(·)는 ReLU 함수.
• Complexity Analysis
  • 단순화를 위해, 우리는 모든 deep layer가 동일한 크기라고 가정
  • Ld는 깊은 층의 수를 나타내고, m은 깊은 층의 크기를 나타낸다.
  • 심층 네트워크의 매개변수 숫자는 d × m + m + (m^2 + m) × (Ld − 1)

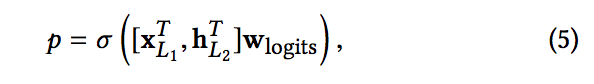
2-4. Combination Layer

• 조합 레이어는 두 네트워크의 출력을 연결합니다.
• 연결된 벡터를 표준로그 레이어에 concatenates 할 수 있습니다. 다음은 두 가지 클래스 분류 문제에 대한 수식입니다.

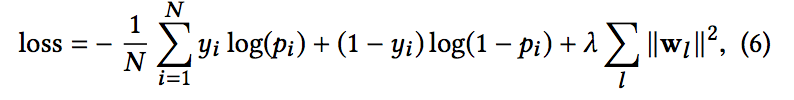
• 여기서 xL1 ∈ Rd, hL2 ∈ Rm은 교차망으로부터의 출력, 딥 네트워크 각각에서, wlogits ∈ R (d + m)은 가중치. sigma(x) = 1 / (1 + exp (-x)) 손실 함수는 정규화항과 함께 로그 손실

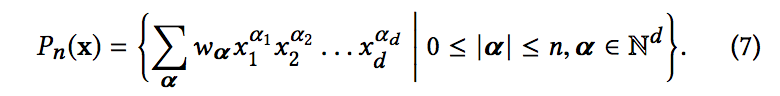
• pi는 방정식 5에서 계산된 확률이고, yi는 실제 레이블이고, N은 총 입력 수이며, λ는 L2 정규화 매개 변수입니다.
• 훈련 과정에서 각 개별 네트워크가 다른 네트워크를 인식할 수 있도록 두 네트워크를 공동으로 훈련합니다.

3. CROSS NETWORK ANALYSIS

• 이 섹션에서는 효율성을 이해하기 위해 DCN의 교차 네트워크를 분석합니다. 1. 다항 근사법, 2. FM에 대한 일반화, 3. 효율적인 투영이라는 세 가지 관점을 제시합니다.
• 간단히 하기 위해 bi = 0 이라고 가정합니다. wj의 i 번째 요소를 wj(i)라고 하자.
• 교차항 (단항) x1^α1 × x2^α2 … xd^αd의 차수는 α로 정의된다. 다항식의 차수는 용어의 가장 높은 정도에 의해 결정됩니다.

3.1 Polynomial Approximation

• Weierstrass 근사 정리[13]에 따르면, 특정 매끄러운 가정 하에서 모든 함수는 다항식으로 임의의 정확도로 근사될 수 있습니다.
• 따라서 다항 근사법의 관점에서 크로스 네트워크를 분석한다. 특히, 교차 네트워크는 효율적이고, 표현적이고, 일반화된 방식으로 같은 정도의 다항식 클래스를 근사화합니다
• 실제 데이터 세트보다 우수합니다. 같은 차수의 다항식 클래스에 대한 교차 네트워크의 근사를 자세히 연구합니다. Pn(x)에 의해 차수 n의 다변수 다항식 클래스를 나타냅니다.

• 이 클래스의 각 다항식에는 O(dn) 계수가 있습니다. O(d) 매개변수만으로 교차 네트워크는 같은 차수의 다항식에서 발생하는 모든 교차항을 포함하고 각 항의 계수는 서로 구별됨을 보여줍니다.

3.2. Generalization of FMs

• 크로스 네트워크는 FM와 같이 매개변수 공유의 정신을 가지고 더 깊이있는 구조로 확장합니다.
• FM 모델에서, 피쳐 xi는 가중치 벡터 vi와 연관되고, 크로스 용어 xixj의 가중치는 hvi, vji에 의해 계산된다.
• 두 모델 모두 각 기능에서 일부 매개변수를 학습했습니다.

• 다른 기능과 독립적이며 교차 용어의 가중치는 해당 매개변수의 특정 조합 매개변수 공유는 모델을 보다 효율적으로 만들뿐만 아니라 모델이 보이지 않는 기능 상호 작용을 일반화하고 소음에 보다 강력해질 수 있게 합니다.

• 예를 들어 스파스 기능이 있는 데이터 세트를 가져옵니다. 2 개의 이진 특징들 xi 및 xj가 훈련 데이터, xixj의 학습된 가중치는 예측에 대해 의미있는 정보를 주지 않을 것이다.
• FM은 얕은 구조이며 차수 2의 교차항을 표현하는 것으로 제한됩니다. 반대로 DCN은 모든 교차항을 구성할 수 있습니다.
• 정리 3.1에서 주장된 바와 같이 층 깊이에 의해 결정되는 어떤 상수로 경계 지어진다.
• 따라서 교차 네트워크는 매개변수 공유라는 개념을 단일 계층에서 다중 계층 및 고차 교차 용어로 확장합니다. 상위 차수의 FM과는 달리 교차 네트워크의 매개변수 개수는 입력 차원에 따라 선형적으로 증가합니다

3.3 Efficient Projection

• 각 교차 레이어는 효율적인 방법으로 x0와 x1 사이의 모든 pairwise 상호 작용을 입력 차원으로 다시 투영합니다.
• 교차 레이어에 대한 입력으로 x Rd를 고려하십시오. 크로스 레이어는 먼저 d2 쌍으로 상호 작용하는 xixj를 암시적으로 구성한 다음 메모리 효율적인 방식으로 차원 d에 암시 적으로 다시 투영합니다.
• 그러나 직접 접근법에는 3차 비용이 따릅니다. 크로스 레이어는 비용면에서 차원적으로 비용을 절감할 수 있는 효율적인 솔루션을 제공합니다.
• 실제로는 행 벡터에 모든 d2 쌍단위 상호 작용 xixj contains가 포함된 경우와 동일합니다.

4. EXPERIMENTAL RESULTS

• 이 섹션에서는 일부 DCN의 성능을 평가합니다.

4.1 Criteo Display Ads Data

• Criteo Display Ads2 데이터 세트는 예측을 위한 것 (광고 클릭률)
• 13개의 정수 피쳐와 26개의 카테고리 피쳐가 있으며 각 카테고리의 카디널리티는 높습니다.
• logloss의 0.001 향상은 실질적으로 중요한 것으로 간주됩니다. 대규모 사용자 기반을 고려할 때 예측 정확도가 약간 향상되면 잠재적으로 회사 매출액이 크게 증가할 수 있습니다.
• 7일(11만 레코드)의 11GB 사용자 로그가 포함됩니다. 훈련을 위해 처음 6일간의 데이터를 사용했고, 무작위로 7일 데이터를 동일한 크기의 검증 및 테스트 세트로 나누었습니다.

4.2 Implementation Details

• DCN은 TensorFlow에서 구현되며, DCN 훈련을 위한 구현 세부사항을 간략하게 논의합니다. 데이터 처리 및 포함. 실수 변환은 로그 변환을 적용하여 정규화됩니다.
• 범주적 특징의 경우, 차원 6 x (범주 카디널리티, 1/4)의 조밀한 벡터에 특징을 Embedding합니다.
• 모든 Embedding을 연결하면 차원 벡터가 생성됩니다 (1026).
• 최적화. Adam Optimizer를 사용하여 미니배치 확률적 최적화를 적용했다. batch size는 512로 설정됩니다.
• Batch normalization는 깊은 네트워크에 적용되고 gradient clip norm은 100으로 설정됩니다. 정규화. L2 norm이나 drop out이 효과적이지 않기 때문에 조기에 멈추었다.
• 숨겨진 레이어 수, 숨겨진 레이어 크기, 초기 학습 속도 및 교차 레이어 수에 대한 그리드 검색을 기반으로 결과를 보고합니다.
• 숨겨진 레이어의 수는 2에서 5 사이이며 숨겨진 레이어 크기는 32에서 1024까지입니다. DCN의 경우 교차 레이어 수는 1에서 6 사이입니다.
• 초기 학습 속도는 0.0001에서 0.001까지 0.0001 단위로 조정되었습니다. 모든 실험은 훈련 단계 150,000에서 조기에 멈춤을 적용했는데, 초과 학습이 발생하기 시작했습니다.

4.3 Models for Comparisons

• DCN과 다섯가지 모델을 비교합니다

1) 교차없는 DNN 네트워크 (DNN) 2) 로지스틱 회귀 (LR) 3) 인수 분해 기계 (FM) 4) Wide and Deep Model (W & D) 5) Deep Crossing (DC)

• 임베디드 레이어, 출력 레이어 및 하이퍼 파라미터 튜닝 프로세스는 DCN과 동일합니다. DCN 모델에서 변경된 부분은 교차 레이어가 없다는 것입니다. LR. 분산 로지스틱 회귀 분석을위한 Sibyl 기계학습 시스템을 사용했습니다.

• 정수 피처는 로그 스케일로 이산화되었다. 교차 기능은 정교한 기능 선택 도구로 선택되었습니다.
• 모든 단일 기능이 사용되었습니다. W & D. DCN과는 달리 광범위한 구성 요소는 원시 희소 기능을 입력으로 사용하며 포괄적인 검색 및 도메인 지식을 사용하여 예측 교차 기능을 선택합니다.
• 교차 기능을 선택하는 좋은 방법이 없기 때문에 비교를 건너뛰었습니다.
• DC. DCN과 비교하여 DC는 명시적 교차 기능을 형성하지 않습니다. 주로 stacking & residual unit을 사용하여 implicit crossings를 만듭니다.
• DCN과 동일한 임베딩 (스태킹) 레이어를 적용한 다음 나머지 ReLu 레이어를 사용하여 residual unit 시퀀스에 대한 입력을 생성했습니다.
• residual unit의 수는 1에서 5까지의 형태로 조정되었으며, 입력 치수 및 교차 치수는 100에서 1026 사이

4.4 Model Performance

• 다른 모델의 최상의 성능을 나열합니다. logloss에서 DCN과 DNN을 비교해 보겠습니다.
• 다른 모델의 성능. 최적의 하이퍼 파라미터 설정은 DCN 모델의 경우 크기가 두 개의 깊은 레이어 1024 및 6 개의 교차 레이어, DNN의 경우 크기가 1024 인 5개의 깊이 레이어, 입력이 있는 나머지 unit 5개 DC에 대한 치수 424 및 교차 치수 537, 및 LR 모델에 대한 42 개의 교차 형상.
• 최고의 실적은 가장 깊은 교차 구조로 발견된 것은 교차 네트워크로부터의 고차원 형상 상호 작용이 가치 있다는 것을 암시합니다.

• 우리가 볼 수 있듯이 DCN은 다른 모든 모델보다 훨씬 많은 성능을 발휘합니다. 특히 최첨단 DNN 모델을 능가하지만 DNN에서 소비되는 메모리의 40% 만 사용합니다.

• 표 1 : 다른 모델의 최상의 테스트 로그 손실. “DC”는 교차 횡단, “DNN”은 교차 레이어가 없는 DCN, “FM”은 Factorization Machine 기반 모델, “LR”은 로지스틱 회귀입니다.

• 각 모델의 최적의 하이퍼 매개 변수 설정을 위해 테스트 로그 로스의 평균 및 표준 편차를 10 개 중 하나로 보고 합니다.

• 독립 실행 : DCN : 0.4422 ± 9 × 10-5, DNN : 0.4430 ± 3.7 × 10-4, DC : 0.4430 ± 4.3 × 10-4.

• 보시다시피, DCN은 다른 모델보다 꾸준히 많은 실적을 올리고 있습니다. DCN과 DNN의 비교. 교차 네트워크는 O (d) 개의 추가 매개변수만 도입한다는 점을 고려하여 기존의 DNN인 DCN을 심층 네트워크와 비교하고 메모리 예산 및 손실 내구성을 변화시키면서 실험 결과를 제시합니다.
• 특정 수의 매개 변수에 대한 손실은 모든 학습 속도와 모델 구조 중에서 가장 좋은 유효성 검사 손실로 보고됩니다.
• 두 모델이 동일하기 때문에 Embedding 레이어의 매개변수 수를 계산에서 생략했습니다.
• 표 2는 원하는 logloss 임계 값을 달성하는 데 필요한 최소한의 매개 변수를 보고합니다. 표 2를 보면 바운드된 Degree 기능 인터랙션을 보다 효율적으로 학습 할 수있는 교차 네트워크 덕분에 DCN이 단일 DNN보다 거의 효율적으로 더 효율적인 메모리임을 알 수 있습니다.

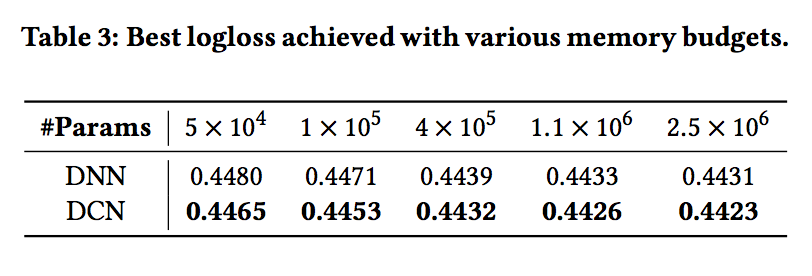
• 표 3은 신경망 모델의 성능을 고정 메모리로 잠음. 보시다시피 DCN은 DNN보다 꾸준히 우위에 있습니다.
• 작은 매개 변수 영역에서 교차 네트워크의 매개변수 수는 깊은 네트워크의 매개 변수 수와 비교할 수 있으며 명확한 개선은 교차 네트워크가 효율적인 피쳐 상호 작용을 학습하는 데보다 효율적임을 나타냅니다.
• 큰 매개 변수 영역에서 DNN은 일부 갭을 닫습니다. 그러나 DCN은 여전히 DNN보다 훨씬 뛰어나므로, 거대한 DNN 모델조차도 할 수없는 의미있는 기능 상호 작용을 효율적으로 학습할 수 있습니다.

• 주어진 DNN 모델에 교차 네트워크를 도입한 효과를 설명함으로써 DCN을 자세히 분석합니다.

• 먼저 DNN과 DCN의 성능을 동일한 수의 레이어 및 레이어 크기로 비교한 다음 각 설정에 대해 더 많은 교차 레이어가 추가 될 때 유효성 검사 로그 손실이 어떻게 변경되는지 보여줍니다.

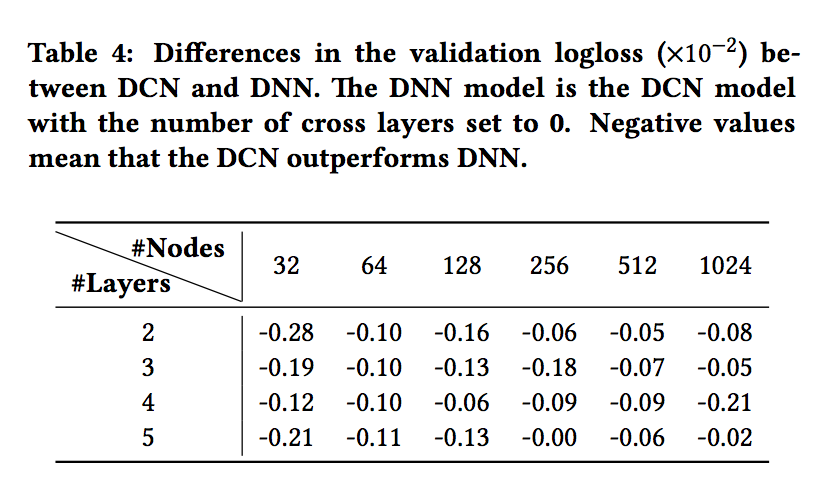
• 표 4는 logloss에서 DCN과 DNN 모델 간의 차이점을 보여줍니다. 동일한 실험 시나리오에서 DCN 모델의 최상의 로그 손실은 동일한 구조의 단일 DNN 모델의 성능보다 지속적으로 우수합니다.
• 개선이 모든 하이퍼 매개 변수에 대해 일관성이 있다는 것은 초기화 및 확률 적 최적화로부터의 무작위 효과를 완화합니다.
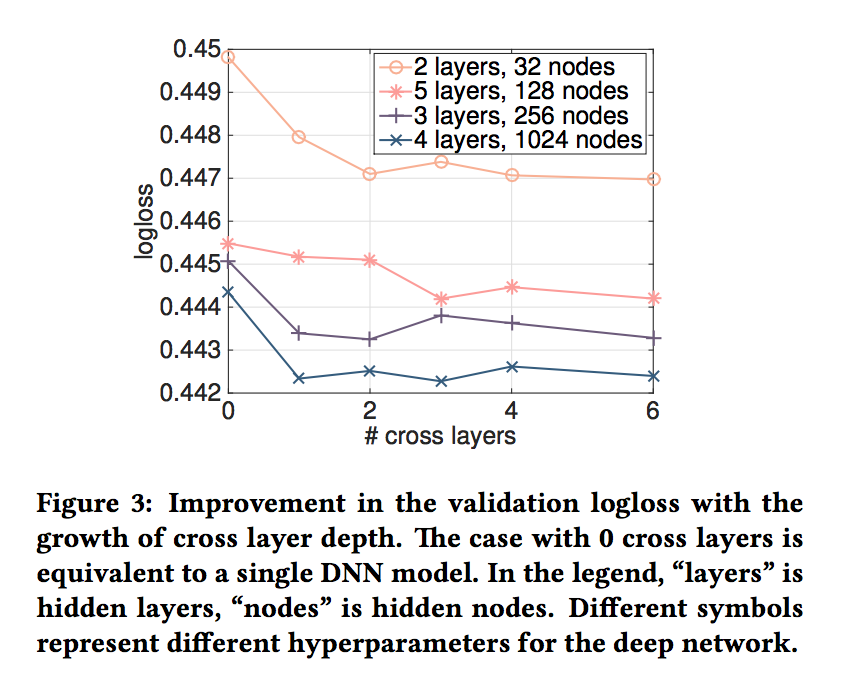
• 그림 3은 무작위로 선택한 설정에서 교차 레이어 수를 늘릴 때의 개선점을 보여줍니다.
• 그림 3의 딥 네트워크의 경우 1 개의 크로스 레이어가 모델에 추가될 때 명확한 개선이 있습니다.
• 더 많은 교차 레이어가 도입됨에 따라 일부 설정의 경우 로그 손실이 계속 감소하여 도입된 교차 용어가 예측에 효과적임을 나타냅니다.
• 다른 한편에서는 로그 손실이 변동하기 시작하고 약간 증가하기도 합니다. 도입된 상위 degree 기능 상호 작용이 도움이 되지 않음을 나타냅니다.

4.5 Non-CTR datasets

• DCN이 비 CTR 예측 문제에서 잘 수행함을 보여줍니다.
• UCI 저장소의 포레스트 코버트 타이프 (581012 샘플 및 54 개 기능) 및 Higgs (11M 샘플 및 28 개 기능) 데이터 세트를 사용했습니다.

• 데이터 세트를 무작위로 교육 (90 %)과 테스트 (10 %)로 나누었습니다. 하이퍼 파라미터에 대한 그리드 검색이 수행되었습니다.

• 깊은 층의 수는 1에서 10 사이이며, 층의 크기는 50에서 300까지이다. 교차 층의 수는 4에서 10까지이다.
• Residual 단위의 수는 입력 치수와 교차 치수가 50에서 1에서 5까지이다

• DCN의 경우 입력 벡터가 교차 네트워크에 직접 공급되었습니다. 포레스트 코 버트 형식 데이터의 경우 DCN은 최소 메모리 소비로 0.9740의 테스트 정확도를 달성했습니다. DNN과 DC 모두 0.9737을 달성했습니다.

• 최적의 하이퍼 파라메터 설정은 DCN의 경우 크기 54 및 크기 6의 깊은 레이어 292 개, DNN의 경우 크기 292 개의 레이어 7 개, DC의 경우 입력 된 크기 271 및 288의 잔여 유니트 4 개입니다.
• Higgs 데이터의 경우 DCN은 0.4494로 가장 좋았으며 DNN은 0.4506을 기록했습니다.
• 최적의 하이퍼 파라메터 설정은 크기 28의 4 개의 교차 레이어와 DCN의 크기 209의 4 개의 깊은 레이어 였고 DNN의 크기는 196 개의 깊은 레이어 10 개였습니다. DCN 성능 향상 (DNN에서 사용되는 메모리의 절반을 차지)

5 CONCLUSION AND FUTURE DIRECTIONS

• 효과적인 피쳐 상호 작용을 확인하는 것이 많은 예측 모델의 성공하지만 유감스럽게도 이 프로세스는 종종 수동 기능 제작 및 철저한 검색이 필요합니다.

• DNNs 자동 기능 학습에 널리 사용됩니다. 그러나 학습된 기능은 암시적이고 비선형 적이며 네트워크가 불필요하게 커지고 특정 기능을 학습하는 데 비효율적 일 수 있습니다.
• 이 논문에서 제안된 Deep & Cross Network는 많은 양의 조밀하고 조밀한 특징을 처리 할 수 ​​있으며, 전통적인 깊은 표현과 함께 결합된 정도의 명시적 교차 특징을 학습합니다.
• 교차 피쳐의 정도는 각 교차 레이어에서 하나씩 증가합니다. 우리의 실험 결과는 모델 정밀도와 메모리 사용량면에서 스파스 데이터 세트와 밀도 데이터 세트 모두에 대한 최첨단 알고리즘보다 우수하다는 것을 보여주었습니다.
• 다른 모델의 블록, 더 깊은 교차 네트워크를 위한 효율적인 훈련을 가능하게 하며, 다항식 근사법에서 교차 네트워크의 효율성을 조사하고, 최적화 동안 깊은 네트워크와의 상호 작용을 더 잘 이해합니다.