코드 원본 및 참고 자료
0. Abstraction
- FM은 feature engineering을 이용해서 대부분의 인수분해 모델을 모방할 수 있기 때문에 일반적인 접근법임.
- 큰 도메인의 범주형 변수들 간의 상호작용들을 추정하는데 있어 FM은 인수분해 모델의 우수성과 피처 엔지니어링의 일반성을 결합함.
- LIBFM은 MCMC(Markov Chain Monto Carlo)를 사용한 베이지안 추정 뿐만 아니라 SGD(stochastic gradient descent)와 ALS(alternating least-squares) 최적화를 지원하는 FM 실행 SW임.
- 이 논문에서는 모델링 및 학습 두 가지 측면에 대한 FM에 대한 최신 연구를 요약하고 ALS 및 MCMC 알고리즘에 대한 확장을 제공하고, 소프트웨어 도구 LIBFM에 대해서 설명함.
1. Introduction
- 최근 FM 관련 연구
- Srebro and Jaakkola 2003 : 두 개의 범주형 변수 간의 관계를 예측
- SVD++,STE,FPMC, timeSVD++,BPTF : 비범주 변수를 고려한 특수 인수 분해 모델들
- SGD, ALS, variational Bayes,MCMC inference: 기본 MF 모델에 대한 많은 학습 및 추론 접근법 (복잡한 문제에서는 주로 GD만이 사용됨)
- 인수분해 모델은 많안 응용 분야들에서 높은 예측 품질을 가지지만
- 범주형 변수로 설명할 수 없는 각각의 문제들에 대해, 새로운 특수 모델을 고안하고 학습 알고리즘을 개발하고 구현해야 함.
- 이 것은 매우 시간이 오래 걸리고, , 인수분해 모델 분야 전문가만 할 수 있음.
- 반면에 실제로 기계학습 분야에서 전형적인 접근 방식은 (피처 엔지니어링으로 전처리 단계를 거쳐) 피처 벡터로 만들고, LIBSVM(서포트벡터머신)이나 weka(선형회귀) 같은 표준 툴에 적용하는 것임.
- 이러한 접근 방식은 기본 머신러닝 모델 및 추론 메커니즘에 대한 지식이 없는 사용자에게도 쉽고, 적용할 수 있음.
- 이 논문에서 다루는 FM은 Factorization Machine(Rendle 2010) 임.
- FM은 인수분해 모델의 높은 예측 정확도와 피처 엔지니어링의 유연성을 결합함.
- FM에 대한 입력 데이터는 선형 회귀와 서포트 벡터 머신 등과 같이 다른 기계학습 접근법과 마찬가지로 실수 값으로 이루전 피처로 이루어져 있음.
- 그러나, FM의 내부 모델은 변수 간의 인수분해된 상호 작용을 사용하여, 다른 추천 시스템에서 처럼 sparse한 환경에서 높은 예측 품질을 제공함.
- 이 논문에서 다룰 내용
- (1) FM 모델과 libFM에서 사용할 수 있는 학습 알고리즘(SGD, ALS)
- (2) 입력 데이터에 대한 몇가지 예시와 특수화된 인수 분해 모델의 관계
- (3) libFM 소프트웨어
- (4) 실험 수행
2. Factorization Machine Model
- 먼저 예측하려고하는 데이터가 설계 행렬 로 표현된다면
- FM 모델은 인수분해된 interaction parameter들을 사용해서 의 입력변수 사이에서 모든 중첩된 상호 작용을 차수 d까지 모델링
-
차수 d=2의 FM 모델은 다음과 같이 정의됨.
- target variable :
- global bias :
- strength of the i-th variable :
- interaction :
- FM 모델에서는 첫번째 부분에서 선형 회귀 모델과 같이 입력 변수 각각과 target에 대한 단항 상호 작용을 포함함.
- 중첩합으로 이루어진 두번째 부분에서는 처럼 input 변수들 간의 모든 쌍의 상호작용을 포함함.
- 표준 다항식 회귀와의 중요한 차이점의 상호작용의 효과가 독립적인 parameter W_{j,j} \thickapprox (v_j, v_{j’}) $$ 로 모델링 됨.
- 위 그림은 실제 추천 문제에 대해 feature vector 를 표현함.
- 파란색 영역 : 사용자에 대한 indicator
- 빨간색 영역 : action item
- 주황색 영역 : 동일한 사용자로부터 매겨진 다른 영화들
- 초록색 영역 : the time in months
- 갈색 영역 : 마지막 영화 등급
-
FM과 표준 기계학습 모델에 대한 관계는 4.3절에서 다룰 예정이며, Section 4. 에서 SVD++, FPMC, timeSVD 등 다른 잘 알려진 인수분해 모델들이 어떻게 FM 모델을 모방하는지(MF를 포함하여) 다룰 예정임.
- 복잡성(Complexity)
- 를 행렬 또는 벡터 의 0이 아닌 요소의 수라고 하면
- indicator function인
- FM 모델은 다음 식과 동등하기 때문에 Equation(1)에서 로 계산됨
- 다선형성(Multilinearity)
- FM의 매력적인 특성은 다선형성임.
- 즉, 각 모델 파라미터 에 대해 FM은 와 두 함수의 선형 결합임.[Rendle et al. 2011]
- 표현력(Expressiveness)
- FM 모델은 어떤 pairwise의 상호작용을 표현할 수 있음(를 충분히 크게 쓴다는 조건 하에)
- 대칭적인 positive semidefinite 행렬 가 로 분해될 수 있음.
- 가 별도의 두 변수 사이의 상호 작용을 표현해야 하는 행렬일 때,
- 는 대칭이며, FM은 대각 요소(diagonal elements)를 사용하지 않으므로 가 positive semidefinite임.
- 실제로 FM의 장점은 의 low-rank 근사를 사용할 수 있기 때문에 FM은 매우 sparse한 데이터에서 상호작용 매개 변수를 예측할 수 있음(4.3절 참조).
- 고차원 FM (Higher-Order FMs)
- 차수 d=2인 FM 모델은 삼항 변수와 고차원 변수의 상호작용들을 인수분해함으로써 확장될 수 있다.
- 고차원 FM 모델은
- 또한 고차원 상호 작용의 경우 식(8)은 보다 효율적은 계산으로 분해될 수 있음.
- 이 논문에서는 2차 FM 다룰 예정임.
- 왜냐면 sparse한 환경(특히 FM이 매력적인)에서 고차원 상화작용들은 일반적으로 추정하기 어려움.
- 그럼에도 불구하고 대부분의 수식과 알고리즘은 2차 FM과 다중선형성을 공유하기 때문에 고차원 FM으로 직접 전이될 수 있음.
3. LEARNING FACTORIZATION MACHINES
FM의 3가지 학습 방법 : SGD [Rendle 2010], ALS[Rendle et al. 2011], MCMC 추론[Freudenthaler et al. 2011]
3.1 Optimization tasks
- 모델 parameter의 최적은 관찰된 데이터 에 대해 손실의 합을 최소화하는 손실 함수 로 대개 정의됨.
-
의 특정 선택에 따라 을 강조하고자 할 대, 모델의 방정식에 parameter 를 추가하고 $$y_hat(x \theta)$$를 쓸 수 있음. - 목적에 따라 손실함수를 선택할 수 있음. 예를 들면 회귀 손실함수는 다음과 같이
- 이진 예측 문제는 시그모이드 로직스틱 함수를 활용할 수 있음.
- FM은 만약 가 충분하다면 대개 많은 parameter 를 가지고 있음.
- 그래서 잘 오버피팅 되기 때문에 L2 정규화가 적용되곤 함.
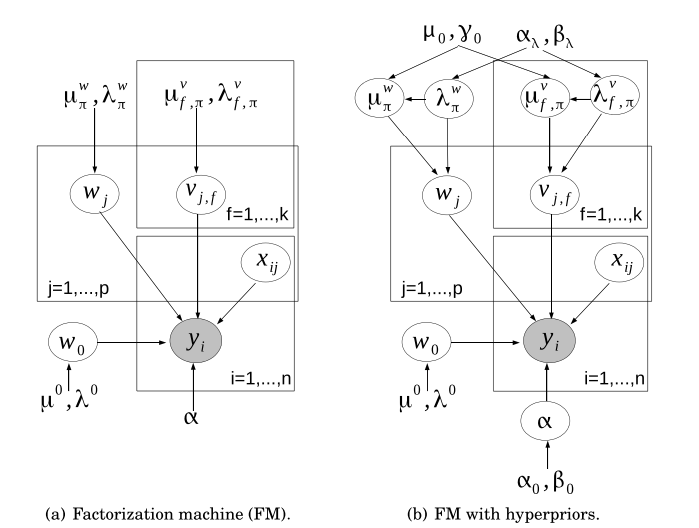
- 확률론적 해석
- 손실과 정규화 둘 다 확률론적인 관점에서 모방되었음.
- 최소 제곱 손실은 가 가우시안 분포를 따른다는 가정 하에 사용됨.
- 이진 분류 문제에서는 베르누이 분포가 가정됨.
-
L2 정규화는 모델 파라미터의 사전분포가 가우시안을 따름.
-
그래서 사전 분포 $$\mu_\theta$는 정규화 값 $\lambda_\theta$와 동일한 방법으로 그룹화되고 구성되어야 함(eq(14).)
-
기울기(Gradients)
- 손실함수를 최적화하는 문제에서 최소제곱회귀 또는 분류를 미분함.
- 최종적으로 FM 모델의 다선형성 때문에 모델의 식이 에 대해 편미분됨.
3.2 Stochastic Gradient Descent
-
SGD 알고리즘은 간단하며 다른 손실함수에 작동을 잘하고 낮은 계산 및 저장 복잡성을 가짐.
- 복잡성
- FM의 SGD 알고리즘은 선형으로 계산될 수 있고 상수 저장 복합성(constant storage complexity)을 가짐.
- SGD의 hyperparameter
- learning rate :
- Regularization :
- Initialization :
- Adaptive Regularization을 사용한 SGD
- SGD에 있어 자동적으로 정규화 값이 자동적으로 조정될 수 있는 방법이 제시[Rendle [2012]]
- libFM에서는 adaptive regularization 알고리즘이 포함되어 있으며, 그룹별로 확장할 수 있음.
3.3 Alternating Least-Squares/Coordinate Descent
3.4 Makov Chain Monte Carlo (MCMC) Inference
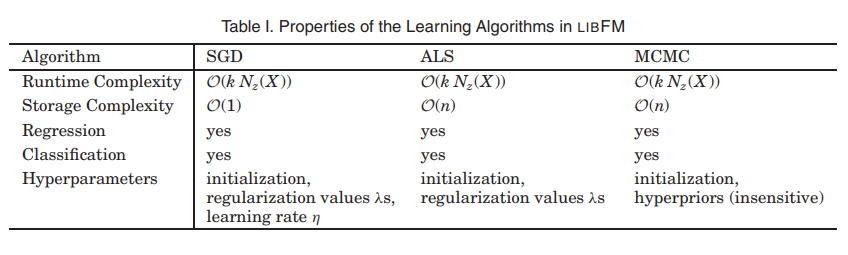
3.5 Summary
- 다음 표는 libFM에서 사용하는 학습 알고리즘의 속성의 개요임.

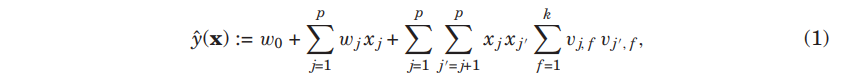
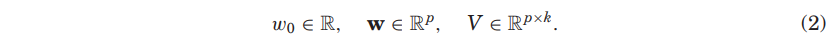

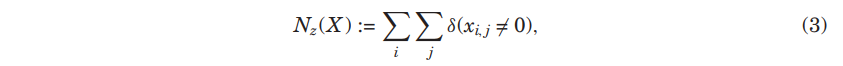
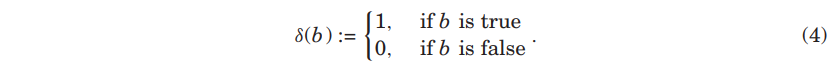
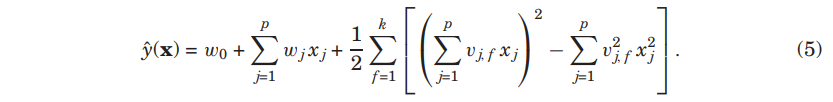


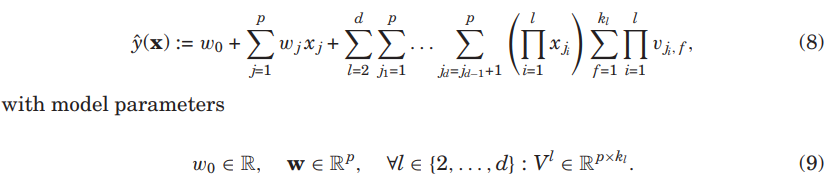
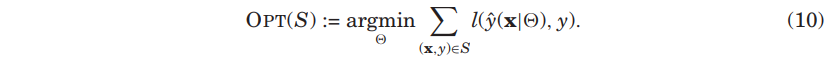
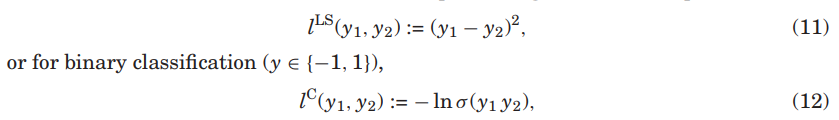
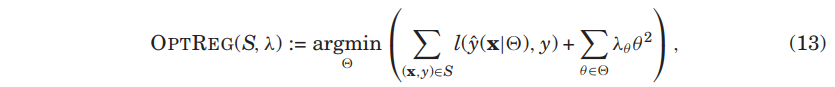
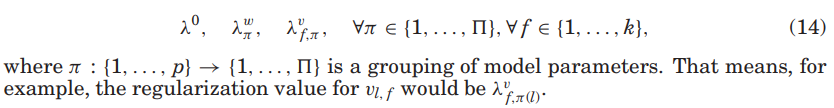

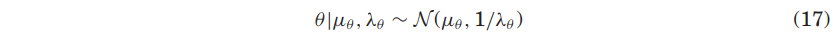







댓글남기기