참고 자료
- 원 논문 (Field-aware Factorization Machines for CTR Prediction)
- FM (Factorization Machine)
들어가기 전에
- Matrix Factorization / Factorization Machine
- CTR Prediction
- 웹 기반 예측에는 카테고리 데이터를 충분히 활용하여 모델링 해야 함
- 일반적인 머신러닝은 카테고리를 ont-hot encoding으로 문제를 푸는데, feature vector들이 highly sparse vector가 되는 문제가 있음
- 이런 feature들을 잘 설명하려면 feature 간의 상호작용을 모델링 하는 것이 중요
- CTR(클릭율) 예측은 광고 문제에서 주로 접근하는 시도 (카카오 광고알고리즘 참고할 것 : https://brunch.co.kr/@kakao-it/84)
- 추천 시스템에서는 eCPM를 계산하여 추천점수 기반으로 랭킹을 매겨야 하는데, eCPM 계산에서 pCTR (예측된 클릭률) 이 필요
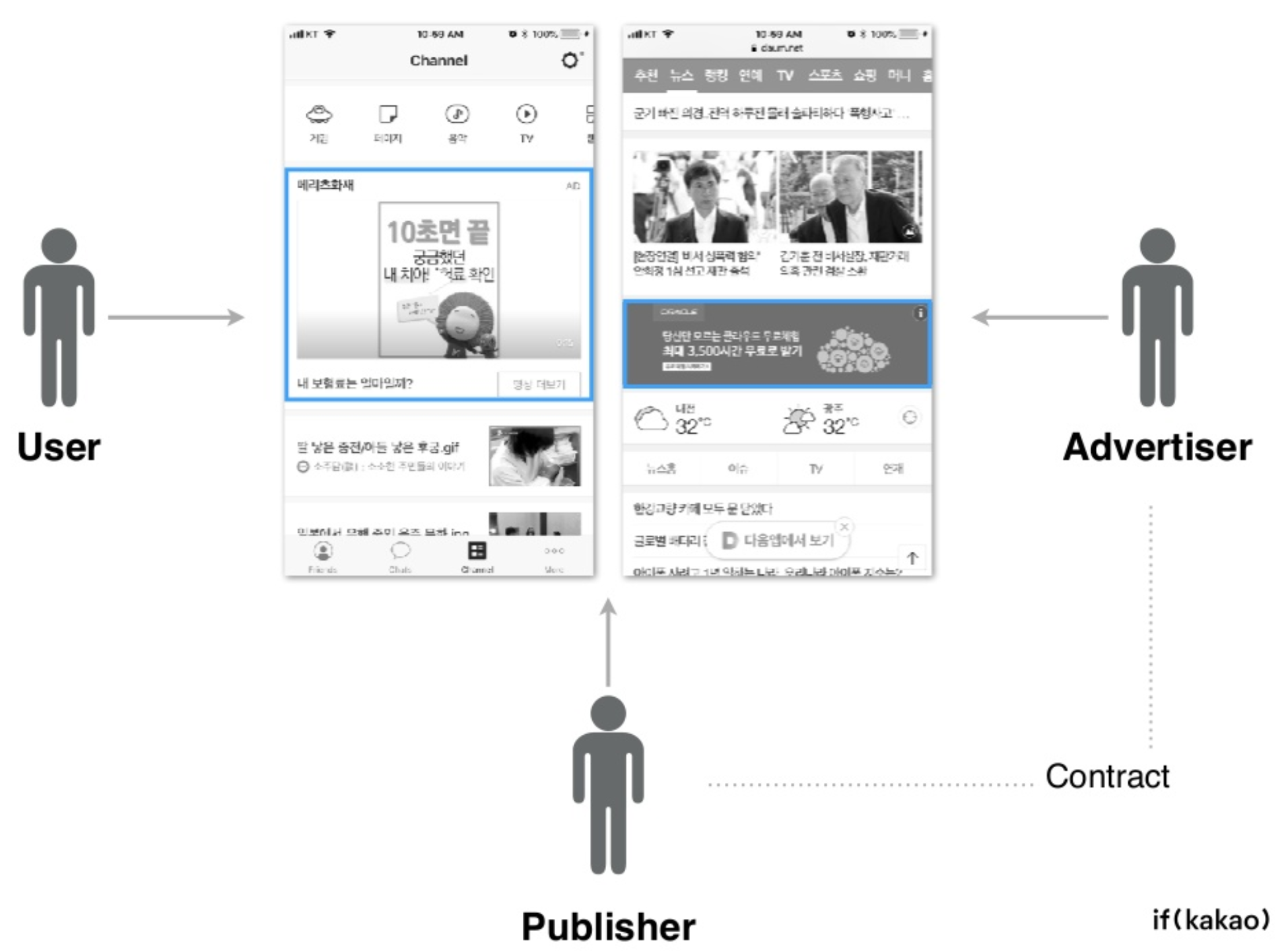

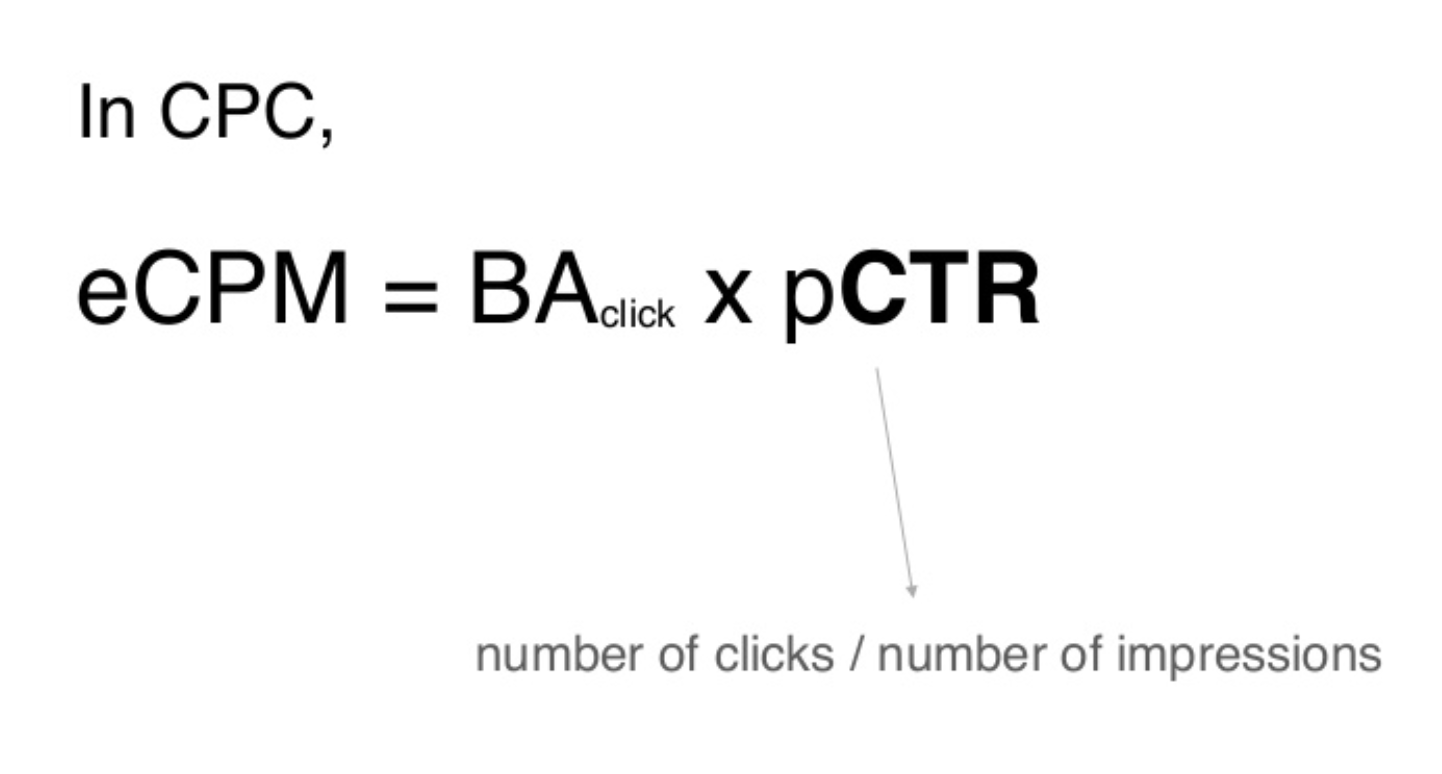
- 추천 시스템에서는 eCPM를 계산하여 추천점수 기반으로 랭킹을 매겨야 하는데, eCPM 계산에서 pCTR (예측된 클릭률) 이 필요
- Factorization models (General)
- 추천 시스템에서 많이 사용하는 하나의 차원축소 방법
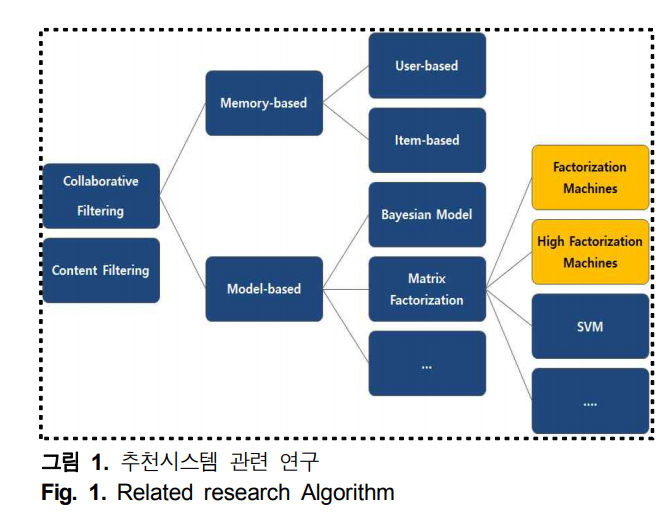
- MF(Matrix Factorization), SVD++, …
- 약점
- not applicable for general prediction tasks
- work only with special input data
- equations and optimization algorithms are derived individually
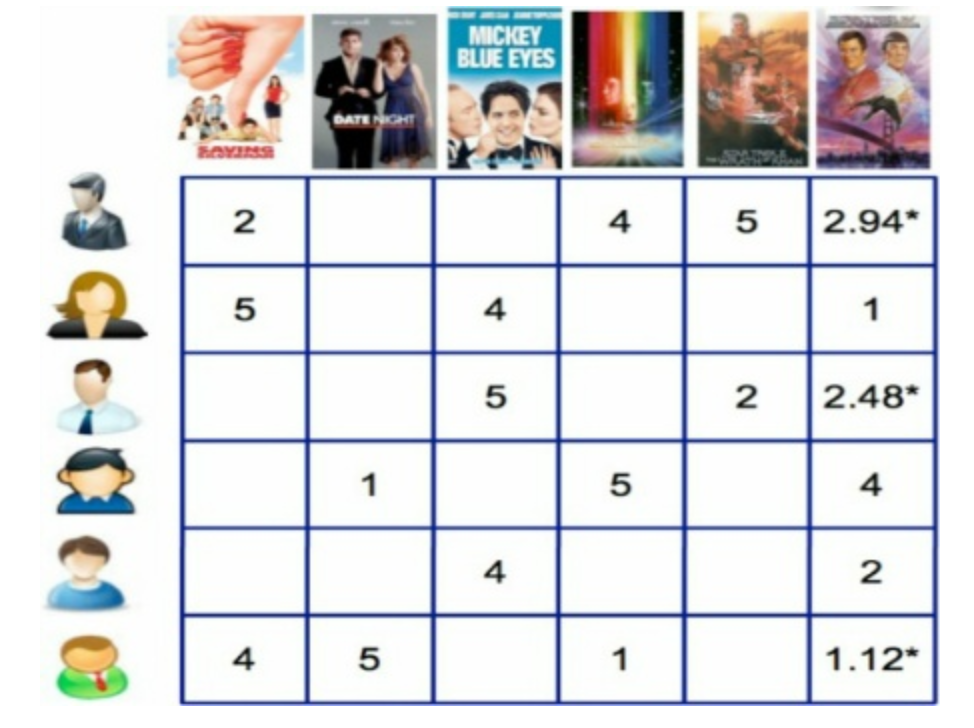
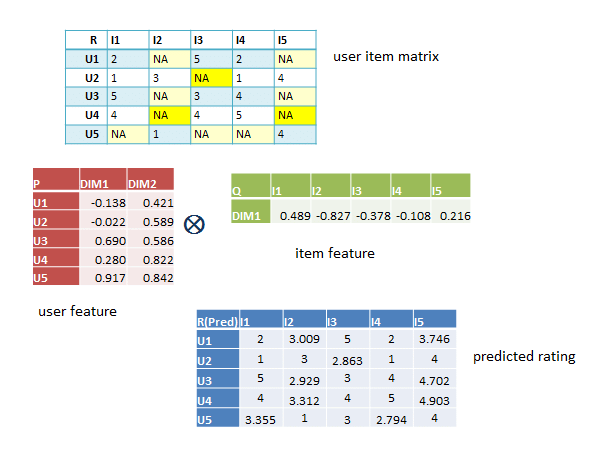
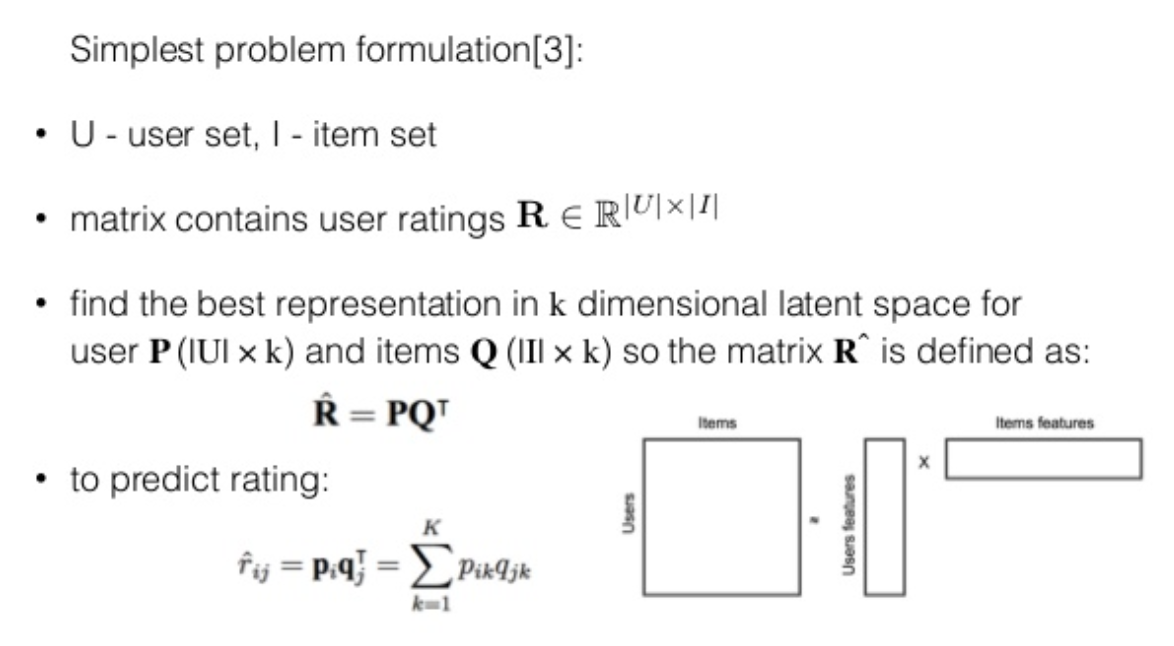
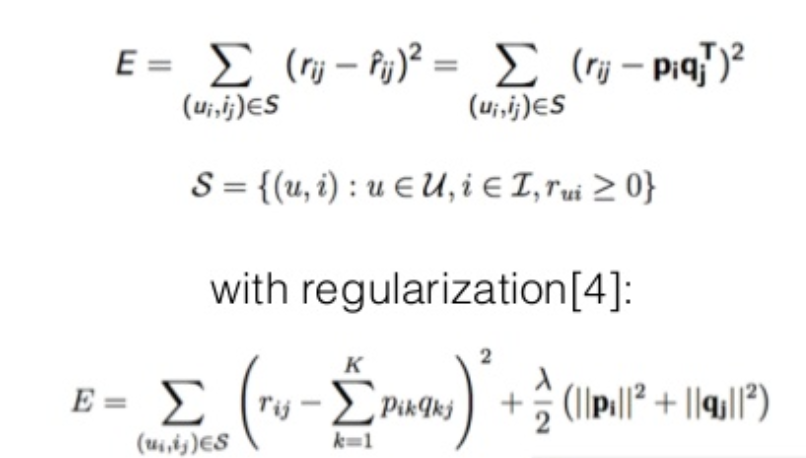
- 추천 시스템에서 많이 사용하는 하나의 차원축소 방법
- Factorization Machine
- FM은 고차원 데이터에서도 제품 변수 간의 상호작용을 통해 효율적으로 사용할 수 있는 지도학습으로 회귀분석과 분류분석 기법을 모두 할 수 있는 기계학습
- 다항식 회귀 또는 커널 방법과 동등하지만, 더 작고 빠른 모델 평가를 통해 정확도를 얻을 수 있음
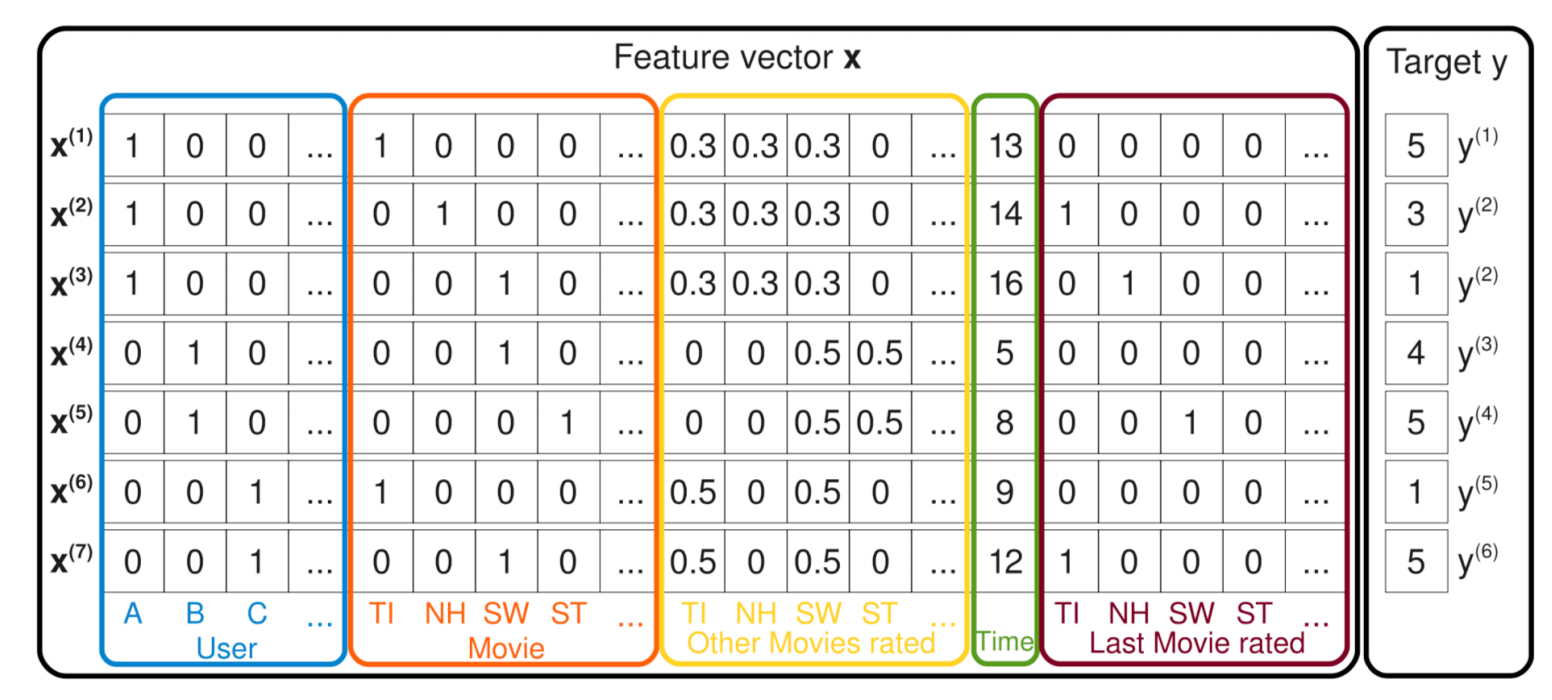

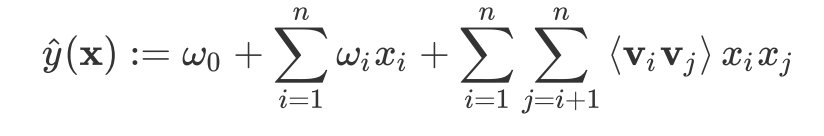
- global (전체 바이어스) + 항목별 바이어스 + 항목별 상호작용
- Factorization machine과 Matrix Factorization의 차이점은 무엇입니까?
- https://stats.stackexchange.com/questions/108901/difference-between-factorization-machines-and-matrix-factorization
- Matrix Factorization 는 행렬을 인수 분해하는 방법입니다. 행렬을 두 개의 행렬로 분해하여 원래의 행렬과 정확하게 일치시키는 작업을 수행합니다.
- Factorization Machine는 선형 모델로 공식화되며 추가 매개 변수로서 Feature 간의 상호 작용이 있습니다.
- Feature 상호 작용은 일반 형식 대신 Latent Vector 표현으로 수행됩니다. Matrix Factorization과 같은 Feature 상호 작용과 함께 다양한 Feature 의 선형 가중치도 사용합니다.
- Matrix Factorization이 일반적으로 사용되는 권장 시스템에서는 side-features을 사용할 수 없습니다.
- 예를 들어 영화 추천 시스템의 경우 Matrix Factorization에서 영화 장르와 언어 등을 사용할 수 없습니다.
- 인수 분해 자체는 기존 상호 작용으로부터 이들을 배워야합니다. 그러나 Factorization Machines에서 이 정보를 전달할 수 있습니다.
- Factorization Machines는 회귀 분석 및 이진 분류와 같은 다른 예측 작업에도 사용할 수 있습니다. Matrix Factorization의 경우에는 그렇지 않습니다.
ABSTRACT
- 클릭률 (CTR) 예측은 컴퓨터 광고에서 중요한 역할을 합니다. 2차 다항식 매핑 및 인수 분해기 (FM)를 기반으로 한 모델이 이 작업에 널리 사용됩니다.
- 최근에는 FFM (Fieldaware Factorization Machine) 인 FM의 변형이 일부 전세계 CTR 예측 경쟁에서 기존 모델을 능가합니다.
- 이 논문에서 우리는 두 가지를 얻은 경험을 바탕으로 CTR 예측을 포함한 대용량 Sparse 데이터를 분류하는 효과적인 방법으로 FFM을 설정합니다.
- 첫째, FFM 훈련을 위한 효율적인 구현을 제안합니다. 다음 FFM을 종합적으로 분석하고 이 접근법을 경쟁 모델과 비교합니다.
- 실험은 FFM이 특정 분류 문제에 매우 유용하다는 것을 보여줍니다
- 마지막으로 일반 대중을위한 FFM 패키지를 출시했음
1. INTRODUCTION
- 클릭률 (CTR) 예측은 광고 업계에서 중요한 역할을 함. 로지스틱 회귀 (logistic regression)가 이 작업에 가장 널리 사용되는 모델.
- m 개의 인스턴스 (yi, xi)가있는 데이터 세트가 주어지면 i = 1,. . . , m 여기서, yi는 레이블이고, xi는 n 차원 특성 벡터이며, 모델 w는 다음 최적화 문제를 해결함으로써 얻어짐.
- 문제 (1)에서, λ는 정규화 매개 변수이고, 손실 함수에서 우리는 선형 모델을 고려
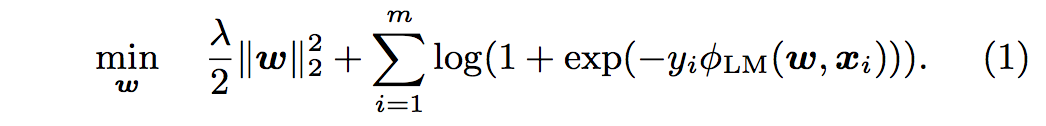
- 피쳐 연결의 효과를 학습하는 것은 CTR 예측에 결정적인 것으로 보입니다.
- 예를 들어, 표 1의 인공 데이터 세트를 사용하여 피쳐 연결을 더 잘 이해할 수 있습니다. Gucci의 광고는 Vogue의 CTR이 특히 높습니다.
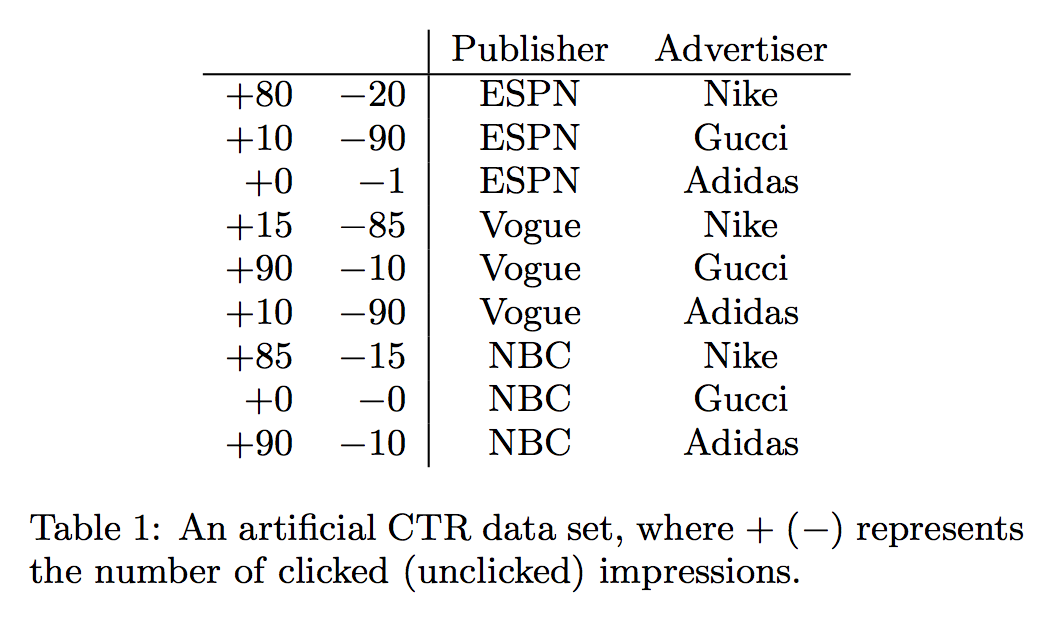
- 그러나 이 정보는 Gucci와 Vogue의 두 가지 가중치를 별도로 학습하기 때문에 선형 모델에서는 학습하기가 어렵습니다. 이 문제를 해결하기 위해 두 가지 모델을 사용하여 feature 결합의 효과를 학습했습니다.
- 첫 번째 모델 인 Degree 2 다항식 매핑 (Poly2)는 각 feature 결합에 대한 전용 웨이트를 학습합니다.
- 두 번째 모델 인 factorization machines (FM) [6]는 feature 결합의 효과를 두 개의 latent 벡터의 곱으로 인수 분해하여 효과를 학습한다.
- Poly2 및 FM에 대한 자세한 내용은 2 절에서 논의 할 것
- 개인화된 태그 추천을 위해 Pairwise interaction tensor factorization (PITF)라고 불리는 FM의 변형이 제안되었습니다.

- KDD Cup 2012에서는 “Team Opera Solutions”[8]에 의해 “Factor Model”이라는 PITF의 일반화가 제안되었습니다.
- 이 용어는 너무 일반적이고 factorization machines와 쉽게 혼동 될 수 있으므로 이 논문에서는 이를 “field-aware factorization machines”(FFM)라고 부릅니다.
- PITF와 FFM의 차이점은 PITF는 “사용자”, “항목”및 “태그”등 3 개의 특수 필드를 고려하지만 FFM은 보다 일반적인 개념
- 최적화 문제를 해결하기 위해 stochastic gradient method을 사용합니다. 과도한 피팅을 피하기 위해 one epoch 만 가지고 훈련합니다.
- FFM은 그들이 시도한 6 가지 모델 중에서 가장 잘 수행합니다. 본 논문에서는 CTR 예측을 위한 효과적인 접근 방법으로 FFM을 구체적으로 설정하고자한다.
- 이 연구는 CTR 예측 문제에 FFM을 적용한 유일한 출판 연구 일 수 있습니다. CTR 예측에 대한 FFM의 효과를 더 입증하기 위해 Crytry와 Avazu가 주관하는 두 가지 전 세계 CTR 대회에서 FFM을 주요 모델로 사용했습니다.
- FFM을 두 개의 관련 모델, Poly2 및 FM과 비교합니다. 먼저 FFM이 왜 FM보다 좋은지 개념적으로 토론하고 정확도와 훈련 시간 면에서 차이점을 확인하기 위한 실험을 실시합니다.
- FFM을 훈련하기 위한 기술을 제시합니다. 여기에는 FFM을 위한 효과적인 병렬 최적화 알고리즘과 과도한 피팅을 피하기 위한 조기정지 기능이 포함됩니다.
- 공개 용으로 FFM을 사용할 수 있도록 오픈 소스 소프트웨어를 출시합니다.
2. POLY2 AND FM
- Chang et. al [4]는 degree-2 다항식 매핑이 종종 Feature 결합의 정보를 효과적으로 포착 할 수 있다는 것을 보여주었다.
- 또한 명시된 Degree 2 차 매핑 형식에 선형 모델을 적용하면 훈련 및 테스트 시간이 Kernel 메소드를 사용하는 것보다 훨씬 빠를 수 있음을 보여줍니다.
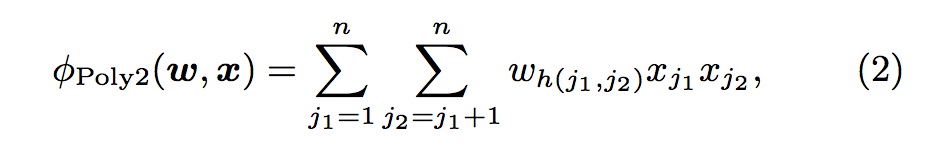
- 여기서, h (j1, j2)는 j1 및 j2를 자연수로 인코딩하는 함수이다.
- 컴퓨팅의 복잡도는 O (n2)입니다. 여기서 n은 인스턴스 당 0이 아닌 요소의 평균 개수입니다.
- FM은 각 특징에 대한 latent 벡터를 암시적으로 학습한다. 각각의 latent 벡터는 k 잠재 인자를 포함하며, 여기서 k는 사용자 지정 파라미터이다.
- 그런 다음 피쳐 연결의 효과는 두 개의 latent 벡터의 내적에 의해 모델링됩니다.
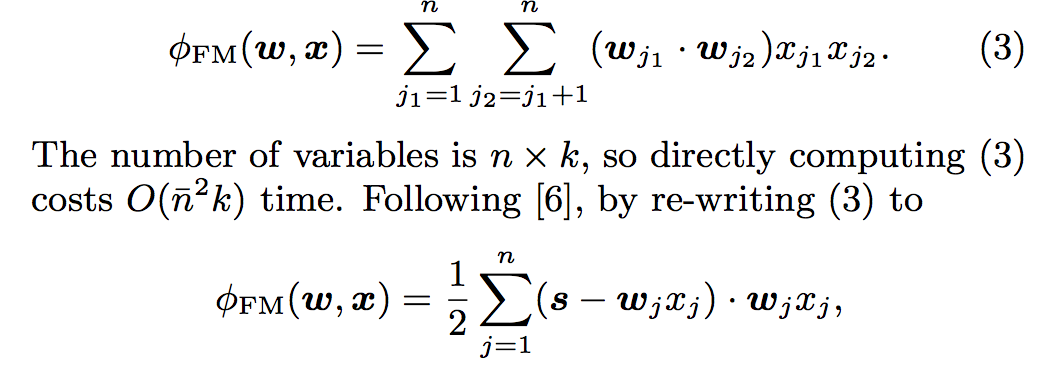
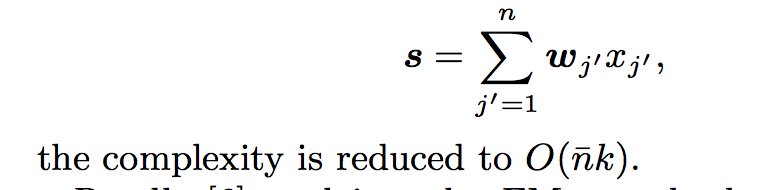
- 그런 다음 피쳐 연결의 효과는 두 개의 latent 벡터의 내적에 의해 모델링됩니다.
-
Rendle [6]은 왜 데이터 세트가 희소 한 경우 FM이 Poly2보다 우수 할 수 있는지 설명합니다. 표 1에 있는 데이터 세트를 사용하여 유사한 그림을 제공합니다.
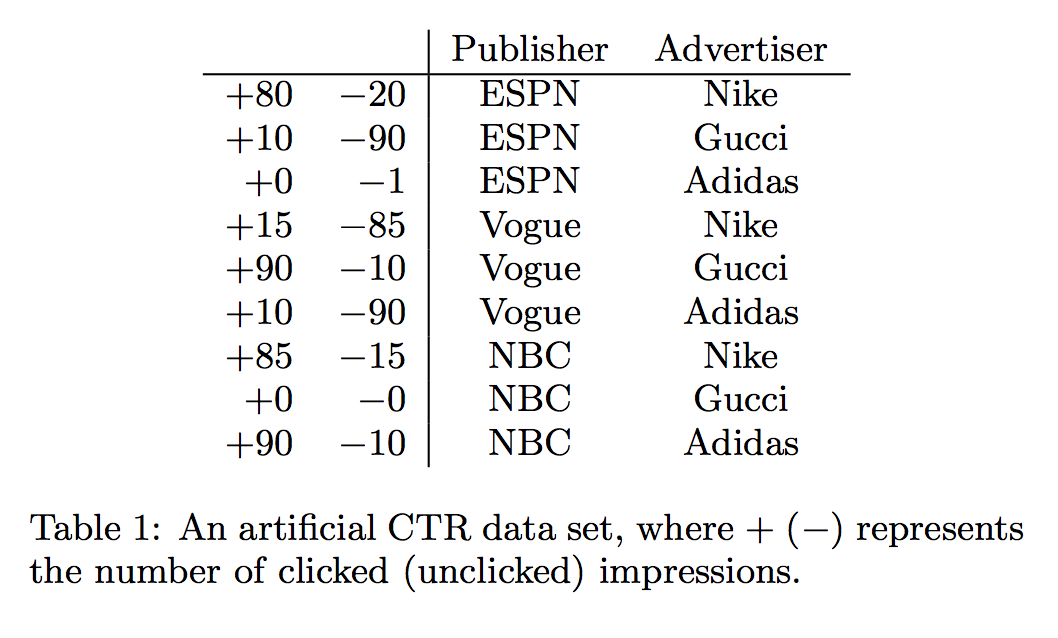

- 예를 들어 쌍 (ESPN, Adidas)에 대한 부정적인 훈련 데이터는 하나뿐입니다. Poly2의 경우 매우 낮은 웨이트 (wespN) 인 Adidas는 이 쌍에 대해 배울 수 있습니다.
- FM의 경우, (ESPN, Adidas)의 예측은 wESPN · wAdidas에 의해 결정되고 wESPN 및 wAdidas는 다른 쌍 (예 : (ESPN, Nike), (NBC, Adidas))에서도 학습되기 때문에 예측은 더 정확한. 또 다른 예는 쌍 (NBC, Gucci)에 대한 훈련 데이터가 없다는 것입니다.
- Poly2의 경우 이 쌍에 대한 예측은 간단하지만 FM의 경우 wNBC 및 wGucci는 다른 쌍에서 배울 수 있기 때문에 의미있는 예측을 수행 할 수 있습니다.
- Poly2에서 h(j1, j2)를 구현하는 순진한 방법은 모든 피쳐 쌍을 새로운 피쳐로 고려하는 것
- 해당 접근법은 O (n2)만큼 큰 모델을 요구한다. 매우 큰 n 때문에 CTR 예측에 일반적으로 비실용적입니다.
- 널리 사용되는 기계학습 패키지인 Vowpal Wabbit (VW) 은 j1과 j2를 해싱하여 이 문제를 해결합니다. 구체적으로 우리의 구현은 VW의 접근 방식과 유사합니다.
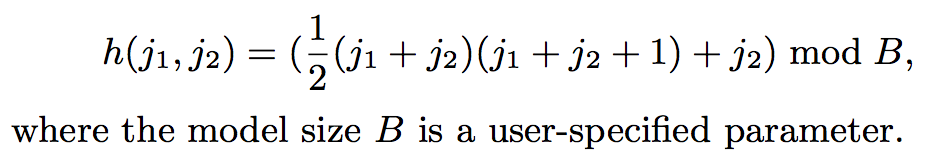
3. FFM
- FFM의 아이디어는 개인화된 태그가 있는 추천 시스템을 위해 제안된 PITF에 기인합니다
- PITF에서는 사용자, 항목 및 태그를 포함하여 세 개의 사용 가능한 필드를 가정하고
- User, Item, and Tag, and factorize (User, Item), (User, Tag), and (Item, Tag)를 separate latent spaces 함
- 그들은 더 많은 필드 (예 : AdID, AdvertiserID, UserID, QueryID)에 대해 PITF를 일반화하고 효과적으로 CTR 예측에 적용
- 세 가지 특정 필드 (사용자, 아이템, 태그)로 제한되며 FFM에 대한 자세한 논의가 부족하기 때문에 이 섹션에서는 CTR 예측에 관한 FFM에 대해보다 포괄적인 연구를 제공합니다.
- 표 1과 같은 대부분의 CTR 데이터 세트의 경우 “기능”을 “필드”로 그룹화 할 수 있습니다.
- 예에서는 ESPN, Vogue 및 NBC의 세 가지 기능이 Publisher 필드에 속하며 다른 세 가지 기능인 Nike, Gucci, 및 Adidas는 Advertiser 필드에 속해 있습니다.
- FFM은 이 정보를 이용하는 FM의 변형입니다. FFM의 작동 방식을 설명하기 위해 다음과 같은 새로운 예를 고려합니다.
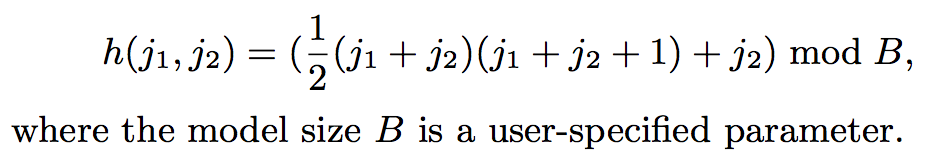

- FM에서 모든 피처는 다른 피쳐와 함께 latent 효과를 배우기 위해 하나의 latent 벡터 만 갖습니다.
- ESPN을 예로 들자면, wESPN은 Nike (wESPN · wNike)와 Male (wESPN · wMale)의 latent 효과를 배우는 데 사용됩니다.
- 그러나 Nike와 Male은 서로 다른 필드에 속하기 때문에 (EPSN, Nike)와 (EPSN, Male)의 latent 효과는 다를 수 있습니다.
- FFM에서, 각 피처는 몇 개의 latent 벡터를 가지고있다. 다른 기능의 필드에 따라 이 중 하나가 내부 기능을 수행하는 데 사용됩니다.
- 위의 예에서 φ FFM (w, x)는 Nike가 필드 광고주에 속해 있기 때문에 (ESPN, NIKE), wESPN, A의 latent 효과를 배우려면 ESPN이 필드 게시자에 속하기 때문에 w를 사용합니다.
- 다시 말하지만, (EPSN, Male)의 잠재 효과를 배우려면 Male이 Gender 필드에 속해 있고 ESPN이 필드 게시자에 속하기 때문에 wMale, P가 사용되었으므로 wESPN, G가 사용됩니다.
- ESPN을 예로 들자면, wESPN은 Nike (wESPN · wNike)와 Male (wESPN · wMale)의 latent 효과를 배우는 데 사용됩니다.
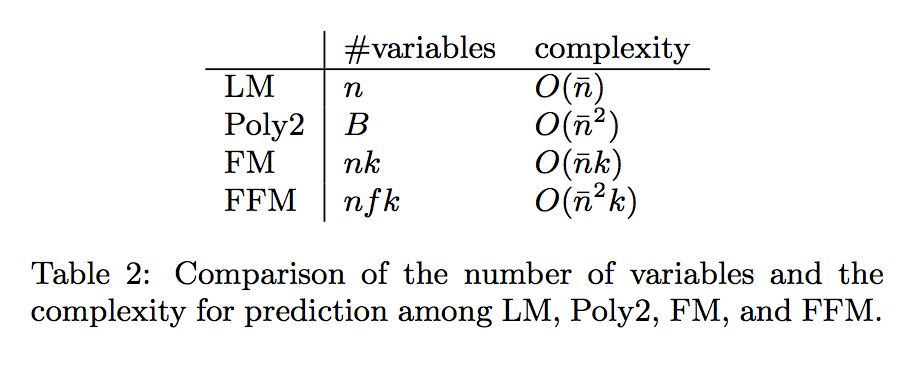
- 여기서 f1과 f2는 각각 j1과 j2의 필드입니다.
- f가 필드의 수인 경우, FFM의 변수의 수는 nfk이며 계산 (4)의 복잡도는 O (n^2 k)입니다. FFM에서는 각 잠재 벡터가 특정 필드의 효과만 학습하면되므로 유의할 필요가 없습니다.



FM : <label> <feature1>:<value1> <feature2>:<value2> …
FFM : <label> <field1>:<feature1>:<value1> <field2>:<feature2>:<value2>

3-1. Solving the Optimization Problem
- 최적화 문제는 φLM (w, x) => φFFM (w, x)로 대체된다는 것을 제외하고 동일
- 확률적 방법 (SG)을 사용한다. 최근 SG의 훈련 과정을 향상시키기 위해 adaptive learning-rate schedules이 제안되었다. FFM의 특별한 경우인 행렬인수 분해에 대한 효과를 보여주기 때문에 AdaGrad 최적화 방식을 사용합니다.
- SG의 각 단계에서 데이터 포인트 (y, x)는 wj1, f2 및 wj2, f1에서. 애플리케이션에서 x가 매우 희소하기 때문에 크기가 0이 아닌 값으로만 업데이트합니다.
- 먼저, 각 그라데이션 d = 1에 대해 하위 그라데이션이 둘째입니다. . . , k, 제곱된 기울기의 합계가 누적됩니다.
- 여기서 η는 사용자가 지정한 학습 속도입니다. w의 초기 값은 [0, 1 / √k] 사이의 균일 분포로부터 무작위로 샘플링된다.
- G의 초기 값은 큰 값을 방지하기 위해 1로 설정된다. 전체적인 절차는 알고리즘 1에 나와 있습니다. 경험적으로, 각 인스턴스를 단위 길이로 정규화하면 테스트 정확도가 매개 변수에 약간 민감합니다.


3.2 Parallelization on Shared-memory Systems
- 최신 컴퓨터에는 멀티 코어 CPU가 널리 장착되어 있습니다. 이러한 코어가 완전히 활용되면 훈련 시간을 크게 줄일 수 있습니다. 많은 병렬화 접근법 SG가 제안되었다.
- 각 스레드는 잠금없이 독립적으로 실행할 수 있습니다. 특히, 알고리즘 1의 3 행에있는 for 루프가 병렬 처리됩니다. 4.4 절에서 병렬 처리의 효과를 조사하기 위해 광범위한 실험을 실시합니다.
3.3 Adding Field Information

- 널리 사용되는 LIBSVM 데이터 형식을 고려하십시오. 여기서 각 (feat, val) 쌍은 feature index and value을 나타냅니다.
- FFM의 경우 위의 형식을 확장합니다. 즉, 해당 기능을 각 기능에 할당해야합니다. 일부 기능에서는 할당이 쉽지만 다른 기능에서는 가능하지 않을 수도 있습니다. 이 문제는 세 가지 일반적인 기능 클래스에 대해 논의합니다.
1.Categorical Features

- 선형 모델의 경우 범주형 기능은 일반적으로 여러가지 이진 특성으로 변환됩니다.
- 데이터 인스턴스의 경우 범주형 기능의 가능한 값 수에 따라 동일한 수의 이진 특성이 생성되고 그 중 하나만 값이 1이 될 때마다 생성됩니다.
- LIBSVM 형식에서 값이 0 인 기능은 저장되지 않습니다. 모든 모델에 동일한 설정을 적용하므로 이 문서에서 모든 범주형 기능은 여러 모델로 변형됩니다. 이진 파일들. 필드 정보를 추가하려면 각 카테고리를 필드로 간주 할 수 있습니다.
2.Numerical Features

- 논문이 conference에서 받아들여질지를 예측하기 위해 다음의 예를 고려해보십시오.
- 우리는 “컨퍼런스의 수용률 (AR)”, “저자의 H-인덱스 (Hidx)”및 “저자의 인용 횟수 (Cite)”의 세 가지 수치적인 특징을 사용합니다. 필드를 할당하는 방법에는 두 가지가 있습니다. 순진한 방법은 각 기능을 더미 필드로 처리하므로 생성된 데이터는 다음과 같습니다.
- 그러나 더미 필드는 단순히 기능의 중복이기 때문에 유익하지 않을 수 있습니다. 또 다른 가능한 방법은 각 수치적 특징을 범주적으로 이산화하는 것입니다.
- 그런 다음 카테고리 정보에 동일한 설정을 사용하여 필드 정보를 추가 할 수 있습니다. 생성 된 데이터는 다음과 같습니다.
- 여기서 AR 특징은 정수로 반올림된다. 가장 큰 단점은 일반적으로 최상의 이산화 설정을 결정하는 것이 쉽지 않다는 것입니다.
- 예를 들어, 우리는 45.73 “45.7”, “45”, “40”또는 심지어 “int (log (45.73))”로 표시됩니다. 또한 이산 후 일부 정보가 손실 될 수 있습니다.
3. Single-field Features

- 일부 데이터 세트에서는 모든 기능이 단일 필드에 속하므로 기능을 필드에 할당하는 것은 의미가 없습니다.
- 일반적으로이 상황은 NLP 데이터 세트에서 발생합니다. 문장이 좋은 기분을 표현하는지 예측하는 다음 예제를 고려하십시오.
- 이 예에서 유일한 필드는 “문장”입니다.이 필드를 모든 단어에 할당하면 FFM은 FM으로 축소됩니다.
- 독자는 숫자형 기능과 마찬가지로 더미 필드 할당에 대해 질문 할 수 있습니다. FFM의 모델 크기는 O (nf k)이다. 더미 필드의 사용은 f = n이고 n은 종종 거대하기 때문에 실용적이지 않습니다.
4. EXPERIMENTS
- 이 섹션에서는 먼저 4.1 절의 실험 설정에 대한 세부 정보를 제공합니다. 다음 매개 변수의 영향을 조사합니다.
- 우리는 LM 또는 Poly2와 달리, FFM은 에포크의 수에 민감합니다.
- 그러므로 4.3 절에서 우리는 조기에 멈추라는 트릭을 제안하기 전에 이 문제에 대해 자세히 논의한다. 병렬화의 속도 향상은 4.4 절에서 연구된다.
- FFMs의 다양한 특성을 확인한 후, 4.5-4.6 절에서 FFM을 Poly2 및 FM을 포함한 다른 모델과 비교합니다.
- 모두 동일한 SG 방법으로 구현되며, 정확성 외에 훈련 시간을 공정하게 비교할 수 있습니다. 또한 LM / Poly2 및 FM을 교육하기위한 state-of-theart 패키지 LIBLINEAR [14] 및 LIBFM [15]을 비교합니다
4.1 Experiment Settings
- Data Sets
-
- Kaggle 대회에서 2 개의 CTR 세트 Criteo와 Avazu를 주로 고려하지만, 4.6 절에서는 더 많은 세트가 고려됩니다.
- Feature 엔지니어링을 위해 우리는 주로 이기는 솔루션을 적용하지만 복잡한 구성 요소는 제거합니다
- 예를 들어, Avazu의 우승 솔루션은 20 가지 모델의 앙상블을 포함하지만 여기에서는 가장 간단한 솔루션 만 사용합니다.
- 다른 세부 정보는 실험 코드를 확인하십시오. 해싱 트릭은 106 개의 피쳐를 생성하기 위해 적용됩니다.

- 두 데이터 세트 모두 테스트 세트의 레이블은 공개되어 있지 않으므로 훈련 및 검증을 위해 사용 가능한 데이터를 두 세트로 분할합니다.
- 데이터 분할은 테스트 세트가 얻어진다. Criteo의 경우, 마지막 6,040,618 개의 라인이 검증 세트로 사용된다; Avazu는 지난 4,218,938 라인을 선택합니다.
- Va : 위에서 언급 한 유효성 검사 집합입니다.
- Tr : 유효성 검사를 제외하고 설정된 새로운 훈련, 원래의 훈련 데이터로부터 설정된다.
- TrVa : 원래의 훈련 세트입니다.
- Te : 원래의 테스트 세트. 레이블은 공개되지 않으므로 점수를 얻기 위해 예상을 원래 평가 시스템에 제출해야합니다.
-
테스트 세트의 과도한 피팅을 피하기 위해 대회 주최측은 이 데이터 세트를 경쟁 중에 점수가 표시되는 “Public Set”와 경쟁 종료 후에 점수를 사용할 수있는 “Private Set”의 두 가지 하위 세트로 나눕니다. 최종 순위는 개인 집합에 의해 결정됩니다.
- Platform
- 모든 실험은 2 개의 Intel Xeon E5-2620 2.0GHz 프로세서와 128GB 메모리에서 12 개의 물리적 코어가있는 Linux 워크 스테이션에서 수행됩니다.
- Evaluation
- 모델에 따라 Sections에서 도입 된 φLM (w, x), φPoly2 (w, x), φFM (w, x) 또는 φFFM (w, x)에 따라서 logloss 값을 평가 함수로 사용
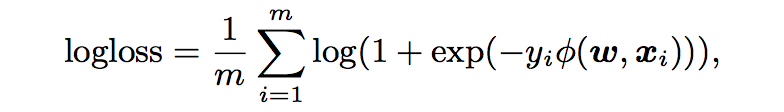
- Implementation
- LM, Poly2, FM 및 FFM을 모두 C ++로 구현합니다. FM 및 FFM의 경우 내부 제품의 효율성을 높이기 위해 SSE 명령어를 사용합니다.
- 논의 된 병렬 처리 섹션 3.2는 OpenMP [16]에 의해 구현됩니다.
- 구현에는 선형 용어와 바이어스 용어가 포함되어 일부 데이터 세트의 성능을 향상시킵니다. 이 용어들이 사용되어야한다. 일반적으로 우리는 해를 끼치 지 않는 것으로 보입니다.
- 코드 확장 성을 위해 필드 정보는 사용된 모델과 상관없이 저장된다는 점에 유의하십시오. FFM 모델이 아닌 경우 필드 정보가 없는 단순한 데이터 구조로 구현이 약간 빨라질 수 있지만 실험 결과는 동일하게 유지되어야 합니다.
4.2 Impact of Parameters
- 파라미터 k, λ 및 η의 영향을 조사하기위한 실험을 수행합니다.
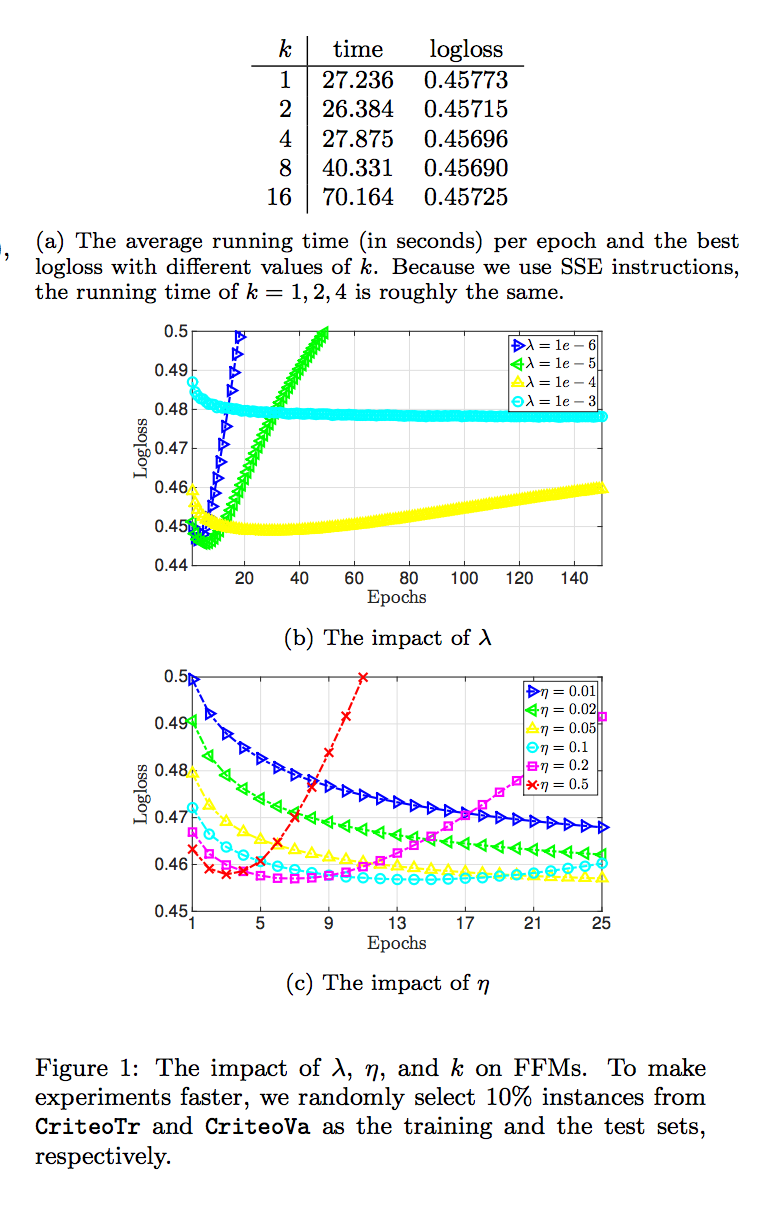
- 결과는 그림 1에서 찾을 수 있습니다. 매개 변수 k와 관련하여 그림 1a의 결과는 로그 손실에 많은 영향을 미치지 않는다는 것을 보여줍니다.
- 그림 1b에서 λ와 logloss 사이의 관계를 나타냅니다. λ가 너무 크면 모델은 좋은 성능을 얻을 수 없습니다.
- 반대로, 작은 λ를 사용하면 모델이 더 나은 결과를 얻지만 쉽게 데이터에 적합합니다. 우리는 훈련 logloss가 계속 감소하는 것을 관찰합니다.
- 매개 변수 η에 대해 그림 1c는 작은 η를 적용하면 FFM이 최상의 성능을 느리게 얻을 수 있음을 보여줍니다.
- 그러나, η가 크면 FFM은 로그 손실을 빠르게 줄일 수 있지만 오버 피팅이 발생합니다. 그림 1b와 1c의 결과로부터 4.3 절에서 논의될 조기 정지의 필요성이 있습니다.
4.3 Early Stopping
- 훈련 데이터에서 최상의 결과를 얻기 전에 훈련 과정을 종료시키는 조기 정지는 많은 기계 학습 문제 [17, 18, 19]에 대한 과도한 피팅을 피하기 위해 사용할 수 있습니다.
- FFM의 경우 우리가 사용하는 전략은 다음과 같습니다.
- 1. 데이터 세트를 학습 세트와 유효성 검증 세트로 분할하십시오.
- 2. 각 epochs의 끝에서 유효성 검증 세트를 사용하여 손실을 계산하십시오.
- 3. 손실이 증가하면 에포크의 수를 기록하십시오. 중지하거나 4 단계로 이동하십시오.
- 4. 필요한 경우 전체 데이터 세트를 사용하여 3 단계에서 얻은 epochs의 수를 사용하여 모델을 다시 훈련시킵니다
- 조기 정지를 적용하는 데 어려움은 logloss가 epochs의 수에 민감하다는 것입니다.
- 그런 다음 유효성 검사 집합에서 가장 좋은 시기는 테스트 집합에서 가장 좋은 시기가 아닐 수 있습니다.
- lazy update5 및 ALS 기반 최적화 방법과 같은 오버 피팅을 피하기 위해 다른 방법을 시도했습니다.
- 그러나 결과는 유효성 검사 세트를 사용하여 조기에 중단 한 결과만큼 성공적이지 못합니다.
- ALS (Alternatvie Least Square) : V 매트릭스에만 임의 값을 채움, V를 고정하고 U를 최적화, U를 고정하고 V를 최적화, 반복하여 원하는 조건을 충족하면 종료
4.4 Speedup
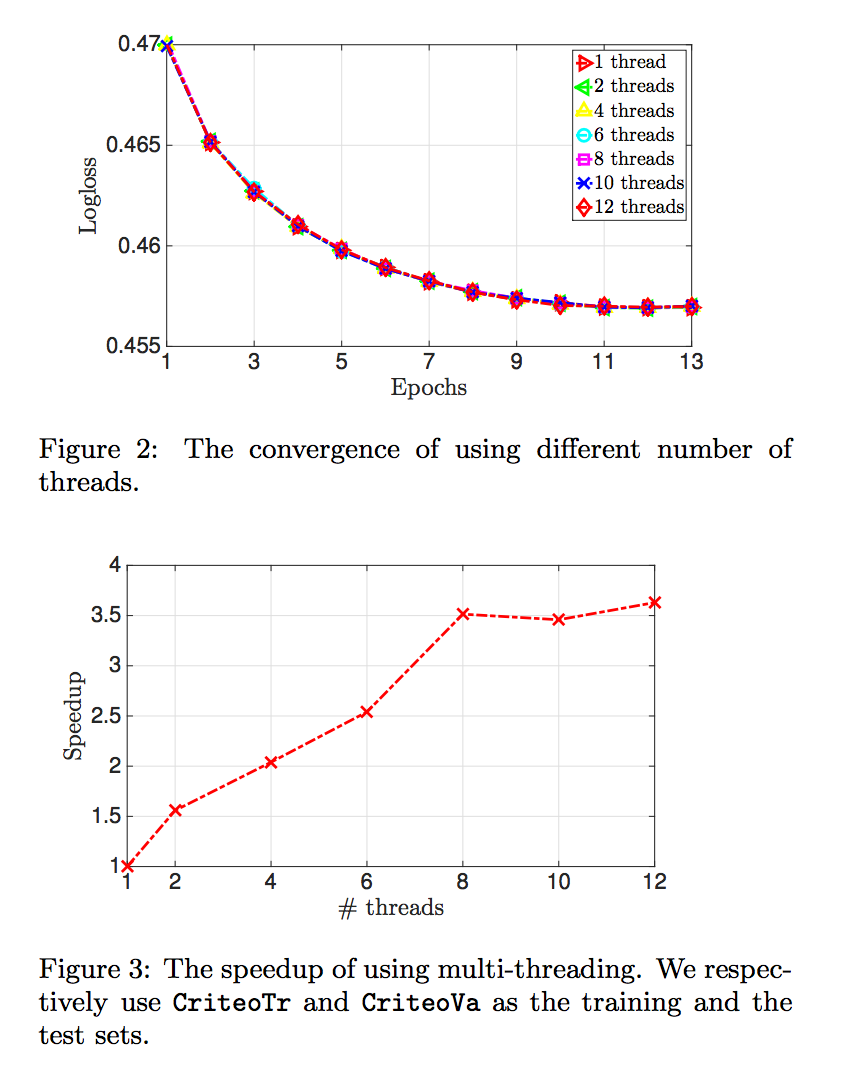
- SG의 병렬 처리가 다른 수렴 동작을 야기 할 수 있기 때문에 그림 2에서 다른 수의 스레드로 실험합니다.
- 결과는 우리의 병렬 처리가 여전히 유사한 수렴 동작을 유도 함을 보여줍니다. 이 속성으로 우리는 speedup을 다음과 같이 정의 할 수있다.
- 그림 3의 결과는 스레드 수가 적을 때 좋은 속도 향상을 보여줍니다. 그러나 많은 쓰레드가 사용된다면, 속도 향상은 별로 좋아지지 않습니다.
- 두 개 이상의 스레드가 동일한 메모리 주소에 액세스 하려고하면 기다려야 한다는 설명이 있습니다. 이러한 종류의 충돌은 더 많은 스레드가 사용될 때 더 자주 발생할 수 있습니다.
4.5 Comparison with LMs, Poly2, and FMs on Two CTR Competition Data Sets
- 공정한 비교를 위해 LM, Poly2, FM 및 FFM에 대해 동일한 SG 방법을 구현합니다.
- 더 나아가, 우리는 두 가지 최첨단 패키지와 비교합니다 :
- LIBLINEAR
- 선형 모델에 널리 사용되는 패키지입니다.
- L2 정규화 된 로지스틱 회귀 분석에서는 두 가지 최적화 방법을 구현합니다.
- 원시 문제를 해결하는 Newton 방법과 해결하기위한 좌표하강 (CD) 방법 이중 문제. 최적화 방법을 확인하기 위해 둘 다 사용했습니다.
- 메소드가 성능에 영향을줍니다. 또한 기존 LIBLINEAR의 Poly2 확장은 해쉬 트릭, 6 그래서 우리는 적절한 수정을 수행하고 이 논문에서 LIBLINEAR-Hash로 표시한다.
- LIBFM
- 인수 분해 기계에 널리 사용되는 라이브러리로서 확률적 경사 방법 (SG), 교대 최소 제곱 (ALS) 및 마르코프 체인 몬테 카를로 (MCMC)와 같은 세 가지 최적화 방법을 지원합니다.
- 이들 모두를 시험해 보았고 ALS가 logloss면에서 다른 두 가지보다 훨씬 우수하다는 것을 발견했습니다. 따라서 우리는 실험에서 ALS를 고려한다.
- 모든 모델의 매개 변수에 대해 점 격자에서 유효성 검사 집합에서 최상의 성능으로 이어지는 매개 변수를 선택합니다. 모든 최적화 알고리즘에는 정지 조건이 필요합니다.
- 우리는 LIBLINEAR에 의한 Newton 방법과 좌표 하강 (CD) 방법의 기본 설정을 사용합니다.
- 다른 모델 각각에 대해, 어떤 반복이 가장 좋은 밸리데이션 스코어로 연결되는지를 확인하기위한 밸리데이션 세트가 필요하다.
- 최선의 반복 횟수를 얻은 후에는 모델을 해당 반복까지 재 훈련합니다.
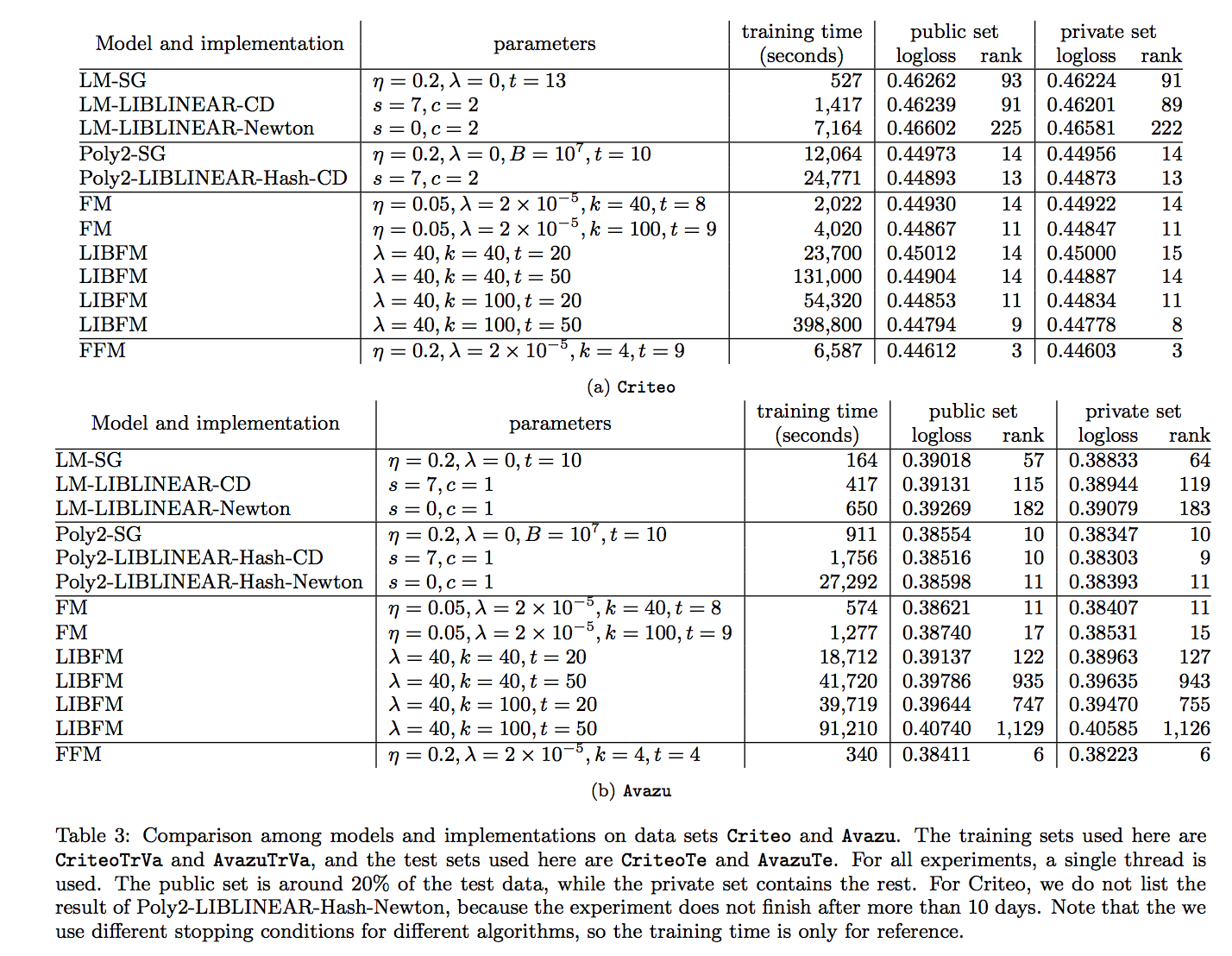
- Criteo와 Avazu의 결과 목록 분명히, FFM은 로그 손실 측면에서 다른 모델보다 우수하지만, LM 및 FM보다 긴 교육 시간도 필요합니다.
- 다른쪽에 LM의 로그 손실은 다른 모델보다 나쁘지만 상당히 빠릅니다. 이 결과는 logloss와 속도 사이의 명확한 절충을 보여줍니다. Poly2는 모두 중에서 가장 느립니다. 모델. 이유는 (2)의 값 비싼 계산 일 수 있습니다.
- FM은 logloss와 속도 사이의 좋은 균형입니다.
- LIBFM의 경우, Criteo에 logloss 측면에서 FMs. 그러나 우리는 우리의 구현이 훨씬 더 빠르다는 것을 알 수 있습니다.
- 우리는 세 가지를 제공합니다. 가능한 이유 : LIBFM에서 사용하는 ALS 알고리즘은 우리가 사용하는 SG 알고리즘보다 복잡합니다. 우리는 SG에서 적응 학습률 전략을 사용합니다. 내부 제품 운영을 향상시키기 위해 SSE 지침을 사용합니다.
- 로지스틱 회귀는 볼록한 문제이므로 이상적으로 LM 또는 Poly2의 경우 3 가지 최적화 방법 (SG, Newton 및 CD)이 전역 최적으로 수렴되는 경우 정확히 동일한 모델을 생성해야합니다.
- 그러나 실제 결과는 약간 다릅니다. 특히, LM by SG는 Avazu의 두 가지 LIBLINEAR 기반 모델보다 낫습니다.
- 구현에서 SG를 통한 LM은 최적화 문제를 느슨하게 해결합니다. 따라서 우리의 실험은 문제가 볼록하더라도 최적화 방법의 중지 조건이 결과 모델의 성능에 영향을 줄 수 있음을 나타냅니다.
4.6 Comparison on More Data Sets
- 이전 섹션에서는 두 개의 경쟁 데이터 세트에 초점을 맞추었지만 다른 데이터 세트에서 FFM이 어떻게 작동하는지 확인하는 것이 중요합니다.
- 이 질문에 답하기 위해 비교를 위해 더 많은 데이터 세트를 고려합니다.
- 대부분의 데이터는 CTR 데이터가 아닙니다. 3.3 절의 논의에 따라 단일 필드 기능이있는 데이터 세트는 고려하지 않습니다.
- 그 이유는 필드 할당 방법에 따라 FFM이 FM과 동등 해 지거나 거대한 모델을 생성하기 때문입니다.
- 여기서 우리는 사용 된 데이터 세트를 간략하게 소개합니다.
- KDD2010- 브리지 : 8이 데이터 세트에는 수치 적 및 범주 적 기능이 모두 포함됩니다.
- KDD2012 : 9이 집합에는 수치 적 및 범주 적 기능이 모두 포함되어 있습니다. 우리의 평가는 logloss이기 때문에 원래의 목표 값인 “클릭 수”를 “클릭 여부”의 이진 값으로 변환합니다.
- cod-rna : 10이 집합은 숫자 기능 만 포함합니다.
- ijcnn : 10이 세트에는 숫자 기능 만 있습니다.
- phishing : 11이 집합은 범주 적 기능 만 포함합니다.
- adult : 12이 데이터 세트에는 숫자 및 범주가 포함됩니다.
- KDD2010- 브리지, KDD2012 및 성인의 경우, 모든 숫자 특징을 29, 13 및 94 개의 빈으로 간단히 이산화합니다.
- cod-rna 및 ijcnn의 경우 기능이 모두 있습니다.
- 수치적으로 우리는 필드 정보를 얻기 위해 3.3 절에서 언급 한 두 가지 접근법을 시도한다 : 더미필드 적용 및 이산화. 매개 변수 선택을 위해 4.5 절의 동일한 절차를 따릅니다.
- 우리는 각 세트를 훈련, 검증 및 테스트 세트로 분리했습니다. 테스트 세트를 예측하기 위해 검증 세트에서 최상의 로그 손실을 달성하는 매개 변수로 훈련 된 모델을 사용합니다.
- 각 데이터 세트의 통계 및 실험 결과는 표 4에 설명되어 있습니다.
- FFM은 KDD2010- 브리지 및 KDD2012의 다른 모델보다 월등히 뛰어납니다. 흔한 이러한 데이터 세트 중 특징은 다음과 같습니다.
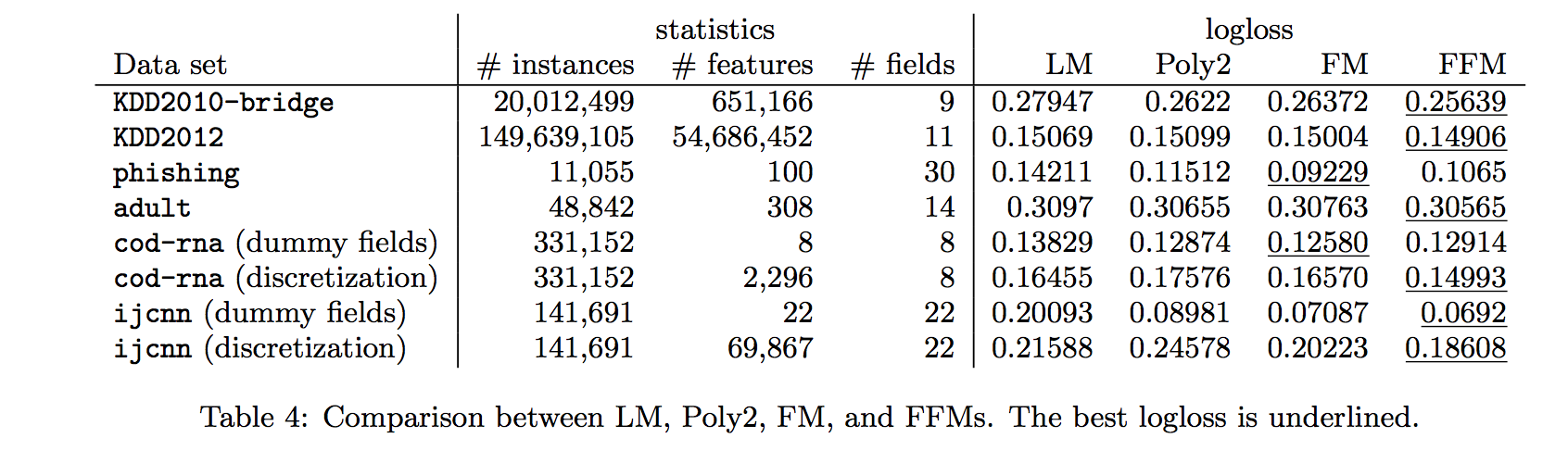
- 결과 집합은 범주적 기능을 많은 바이너리 기능으로 변환한 후 매우 희박합니다.
- 그러나 phishing 및 adult의 데이터 경우 FFM이 크게 향상되지는 않습니다.
- phishing의 경우 데이터가 희박하지 않아 FFM, FM 및 Poly2의 성능이 비슷할 수 있습니다.
- adult의 경우, 모든 모델이 선형 모델과 유사하게 수행되기 때문에 feature 연결이 유용하지 않은 것 같습니다.
- 데이터 세트에 숫자 기능만 있으면 FFM에 분명한 이점이 없을 수 있습니다.
- 더미 필드를 사용하면 FFM은 FM을 초과하여 출력하지 않으므로 필드 정보가 도움이 되지 않습니다.
- 다른 한편으로, 우리가 수치 적 특징을 이산화 시키면, FFM이 최선이지만 모든 모델 중에서 더미 필드를 사용하는 것보다 성능이 훨씬 더 나쁩니다. 다양한 종류의 데이터 세트에 FFM을 적용하는 지침을 요약합니다.
- FFM은 범주적 기능을 포함하고 이진 기능으로 변환되는 데이터 집합에 효과적이어야 합니다.
- 변환된 집합이 너무 적지 않은 경우 FFM은 이점이 적은 것으로 보입니다. 숫자 데이터 세트에 FFM을 적용하는 것이 더 어렵습니다.
5. CONCLUSIONS AND FUTURE WORKS
- 논문에서는 FFM의 효율적인 구현에 대해 논의한다.
- 특정 종류의 데이터 세트의 경우 FFM은 logloss 측면에서 잘 알려진 3 가지 모델 인 LM, Poly2 및 FM보다 성능이 우수하고 훈련 시간이 길다는 것을 입증합니다.
- 앞으로의 연구에서 4.3 절에서 논의된 초과 적합 문제는 우리가 조사 할 문제이다.
- 게다가 구현의 용이성을 위해 SG를 최적화 방법으로 사용합니다. 다른 최적화 방법 (예 : Newton 방법)이 FFM에서 어떻게 작동하는지 보는 것은 흥미롭습니다.




댓글남기기